A linear combination of the splines \(S_j\) in the input object is computed according to
$$R_i=\sum_{j=0}^{d} a_{i j} S_j,\, i=1,\dots, l.$$
and returned as a Splinet-object.
Arguments
- object
Splinetsobject containingdsplines;- A
l x dmatrix; coefficients of the linear transformation,- reduced
logical; If
TRUE(default), then the linear combination is calculated accounting for the actual support sets (recommended for sparse splines), ifFALSE, then the full support computations are used (can be faster for lower dimension or non-sparse cases).- SuppExtr
logical; If
TRUE(default), the true support is extracted, otherwise, full range is reported as the support. Applies only to the case whenreduced=FALSE.
Value
A Splinet-object that contains l splines obtained by linear combinations of
using coefficients in rows of A. The SLOT type of the output splinet objects is sp.
References
Liu, X., Nassar, H., Podg\(\mbox{\'o}\)rski, K. "Dyadic diagonalization of positive definite band matrices and efficient B-spline orthogonalization." Journal of Computational and Applied Mathematics (2022) <https://doi.org/10.1016/j.cam.2022.114444>.
Podg\(\mbox{\'o}\)rski, K. (2021)
"Splinets – splines through the Taylor expansion, their support sets and orthogonal bases." <arXiv:2102.00733>.
Nassar, H., Podg\(\mbox{\'o}\)rski, K. (2023) "Splinets 1.5.0 – Periodic Splinets." <arXiv:2302.07552>
Examples
#-------------------------------------------------------------#
#------------Simple linear operations on Splinets-------------#
#-------------------------------------------------------------#
#Gathering three 'Splinets' objects
n=53; k=4; xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1;Nspl=10
set.seed(5)
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1))
spl=construct(xi,k,S) #constructing the first proper spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The spline 1 'ths highest derivative at the central knot is zero.
#> Now it is set to zero.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.393512 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The matrix derivative is now corrected by method RRM .
spl@epsilon=1.0e-5 #to avoid FALSE in the next function due to inaccuracies
is.splinets(spl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 55 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 1.321823e-13
#>
RS=rspline(spl,Nspl) #Random splines
plot(RS)
A = matrix(rnorm(5*Nspl, mean = 2, sd = 100), ncol = Nspl)
new_sp1 = lincomb(RS, A)
plot(new_sp1)
new_sp2 = lincomb(RS, A, reduced = FALSE)
plot(new_sp2)
#---------------------------------------------#
#--- Example with different support ranges ---#
#---------------------------------------------#
n=25; k=3
set.seed(5)
xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
#Defining support ranges for three splines
supp=matrix(c(2,12,4,20,6,25),byrow=TRUE,ncol=2)
#Initial random matrices of the derivative for each spline
SS1=matrix(rnorm((supp[1,2]-supp[1,1]+1)*(k+1)),ncol=(k+1))
SS2=matrix(rnorm((supp[2,2]-supp[2,1]+1)*(k+1)),ncol=(k+1))
SS3=matrix(rnorm((supp[3,2]-supp[3,1]+1)*(k+1)),ncol=(k+1))
spl=construct(xi,k,SS1,supp[1,]) #constructing the first correct spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.502577 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
nspl=construct(xi,k,SS2,supp[2,])
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.705421 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl,nspl) #the second and the first ones
nspl=construct(xi,k,SS3,supp[3,])
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 - highest derivative is not symmetric at the center (equal values at the two central knots).
#> The two values have been made equal by averaging.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.573415 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 5 knots, the first 2 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 5 knots, the first 2 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl,nspl) #the third is added
A = matrix(rnorm(3*2, mean = 2, sd = 100), ncol = 3)
new_sp1 = lincomb(spl, A) # based on reduced supports
plot(new_sp1)
new_sp2 = lincomb(spl, A, reduced = FALSE) # based on full support
plot(new_sp2) # new_sp1 and new_sp2 are same
#-----------------------------------------#
#--- Example with varying support sets ---#
#-----------------------------------------#
n=40; xi=seq(0,1,by=1/(n+1)); k=2;
support=list(matrix(c(2,9,15,24,30,37),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp1 = is.splinets(sp)[[2]] #the corrected vs. the original 'der' matrices
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 2.084063 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.756979 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 3 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 3 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.558399 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
support=list(matrix(c(5,12,17,29),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp2 = is.splinets(sp)[[2]] #building a valid spline
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.529603 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 support 2 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 2 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.62228 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
spp = gather(sp1,sp2)
support=list(matrix(c(3,10,14,21,27,34),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp3 = is.splinets(sp)[[2]] #building a valid spline
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.843411 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.406557 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 3 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 3 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.161176 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
spp = gather(spp, sp3)
plot(spp)
spp@supp #the supports
#> [[1]]
#> [,1] [,2]
#> [1,] 2 9
#> [2,] 15 24
#> [3,] 30 37
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 5 12
#> [2,] 17 29
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 3 10
#> [2,] 14 21
#> [3,] 27 34
#>
set.seed(5)
A = matrix(rnorm(3*4, mean = 2, sd = 100), ncol = 3)
new_sp1 = lincomb(spp, A) # based on reduced supports
plot(new_sp1)
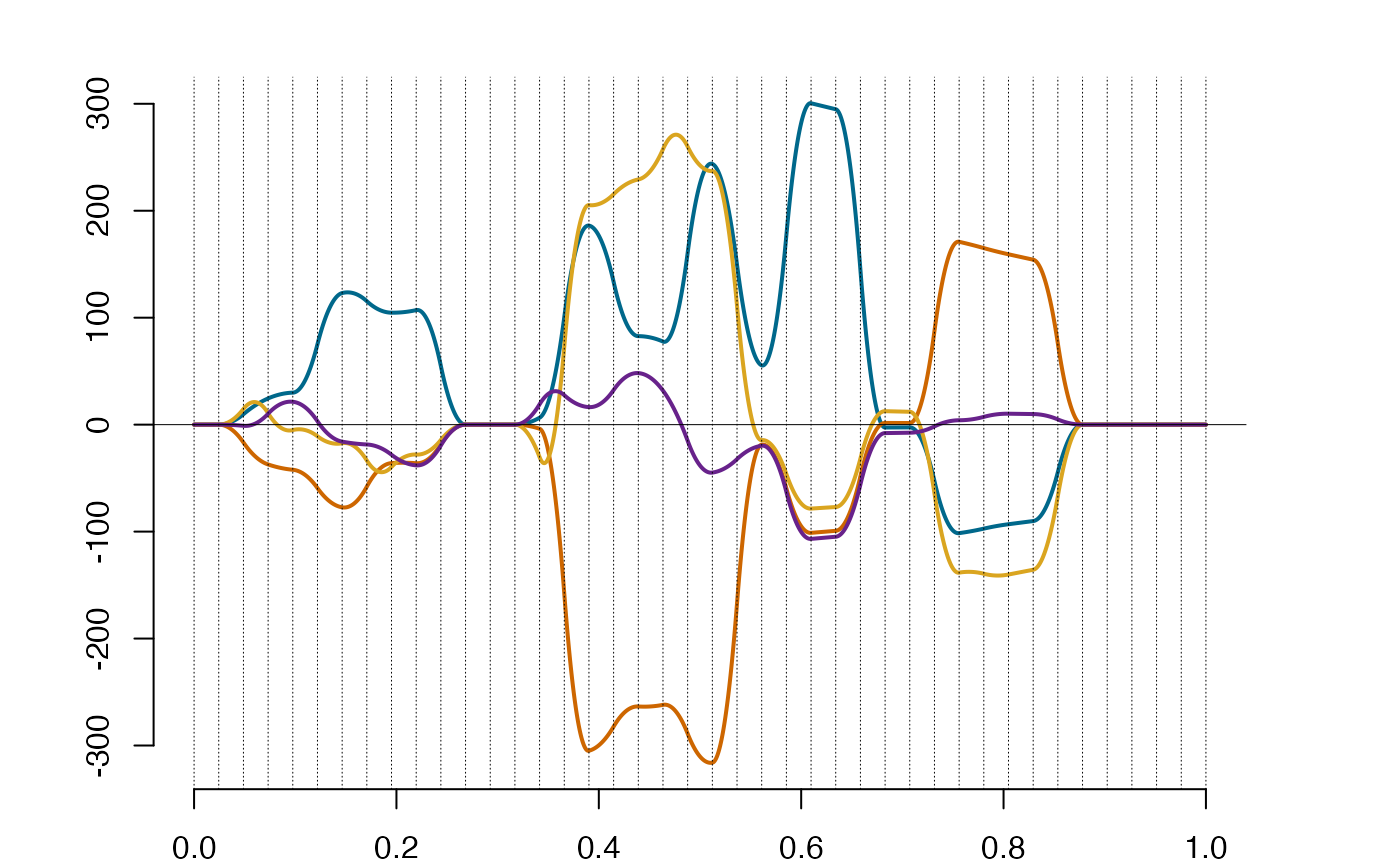new_sp1@supp #the support of the output from 'lincomb'
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
#> [[4]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
new_sp2 = lincomb(spp, A, reduced = FALSE) # based on full support
plot(new_sp2) # new_sp1 and new_sp2 are same
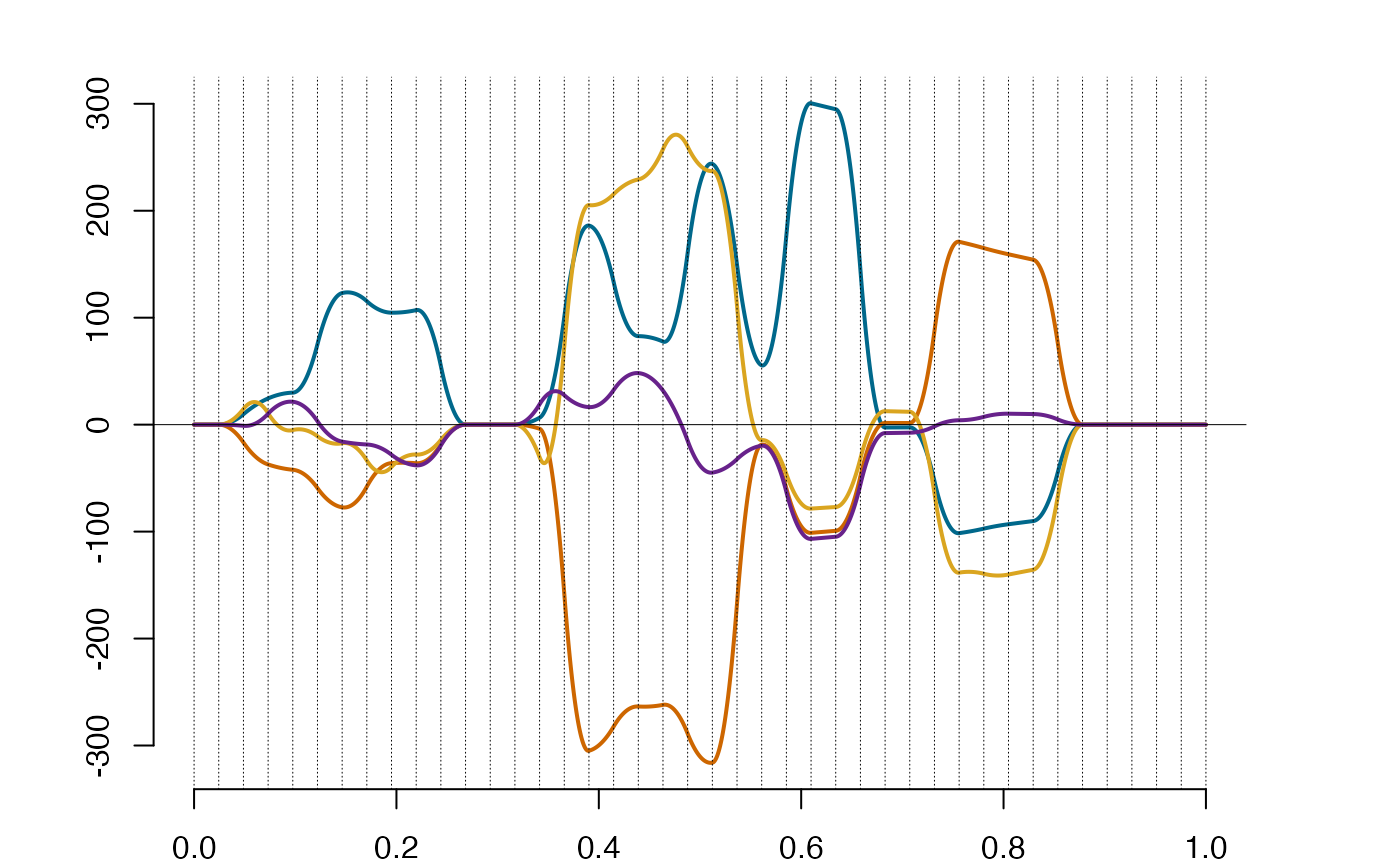new_sp2@supp #the support of the output from 'lincomb' with full support computations
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
#> [[4]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 14 37
#>
#-------------------------------------#
#--- Support needs some extra care ---#
#-------------------------------------#
set.seed(5)
n=53; k=4; xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
supp1 = matrix(c(1, ceiling(n/2)+1), ncol = 2)
supp2 = matrix(c(ceiling(n/2)+1, n+2), ncol = 2)
S = matrix(rnorm(5*(ceiling(n/2)+1)), ncol = k+1)
a = construct(xi,k,S,supp = supp1) #constructing the first proper spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 - highest derivative is not symmetric at the center (equal values at the two central knots).
#> The two values have been made equal by averaging.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.557076 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
S = matrix(rnorm(5*(ceiling(n/2)+1)), ncol = k+1)
b = construct(xi,k,S,supp = supp2) #constructing the first proper spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 - highest derivative is not symmetric at the center (equal values at the two central knots).
#> The two values have been made equal by averaging.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.327398 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
sp = gather(a,b)
plot(sp)
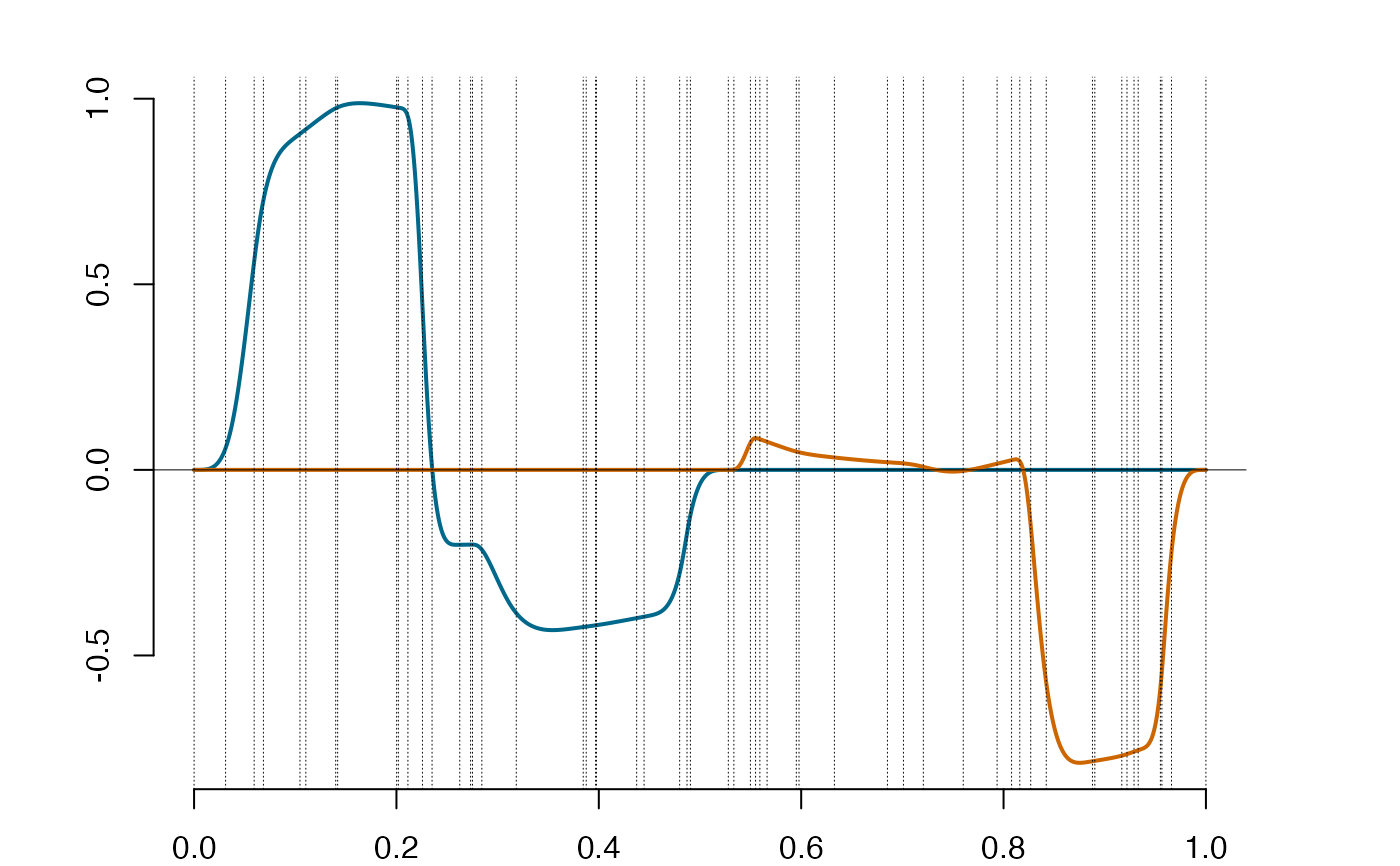# create a+b and a-b
s = lincomb(sp, matrix(c(1,1,1,-1), byrow = TRUE, nrow = 2))
plot(s)
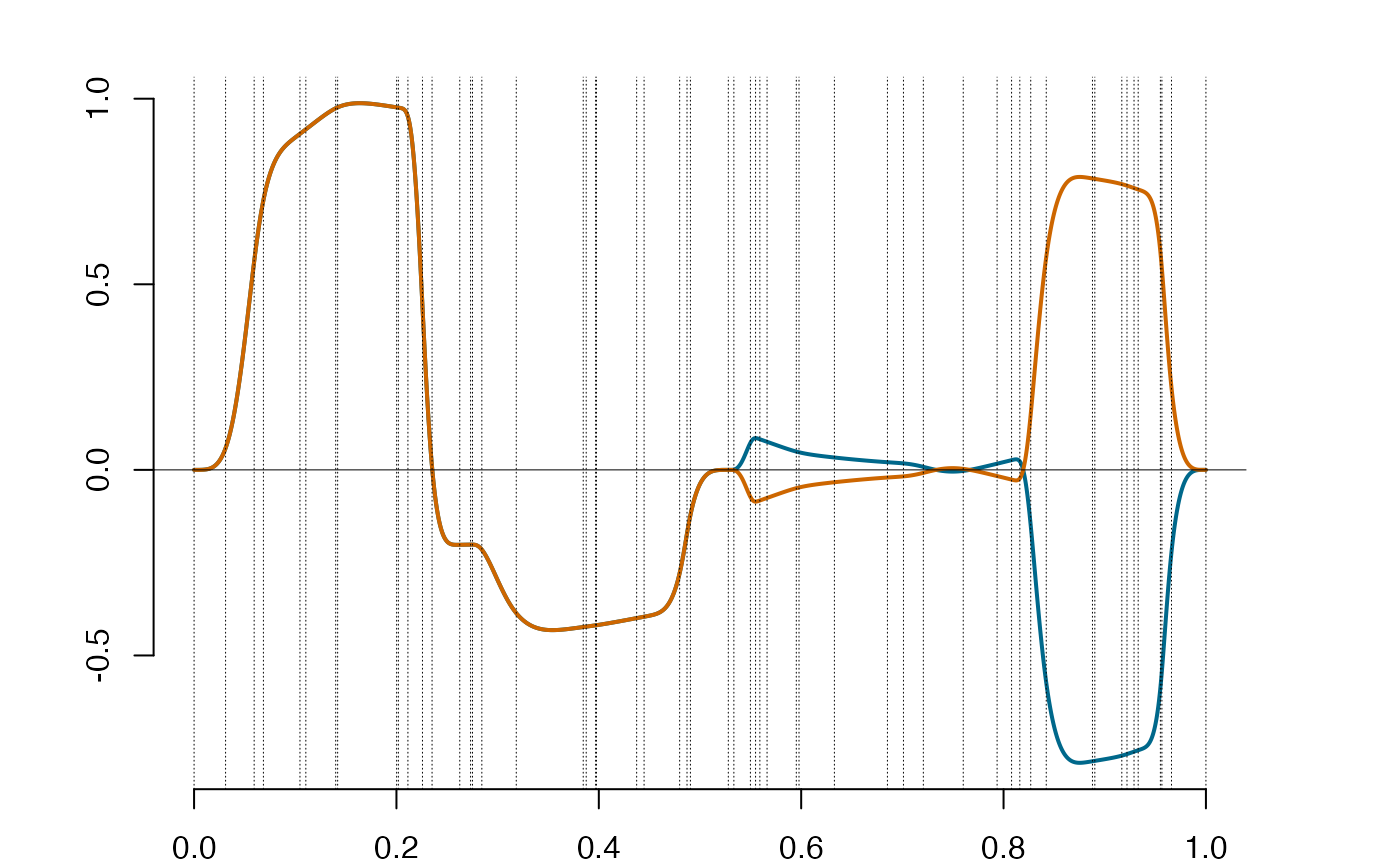s@supp
#> list()
# Sum has smaller support than its terms
s1 = lincomb(s, matrix(c(1,1), nrow = 1), reduced = TRUE)
plot(s1)
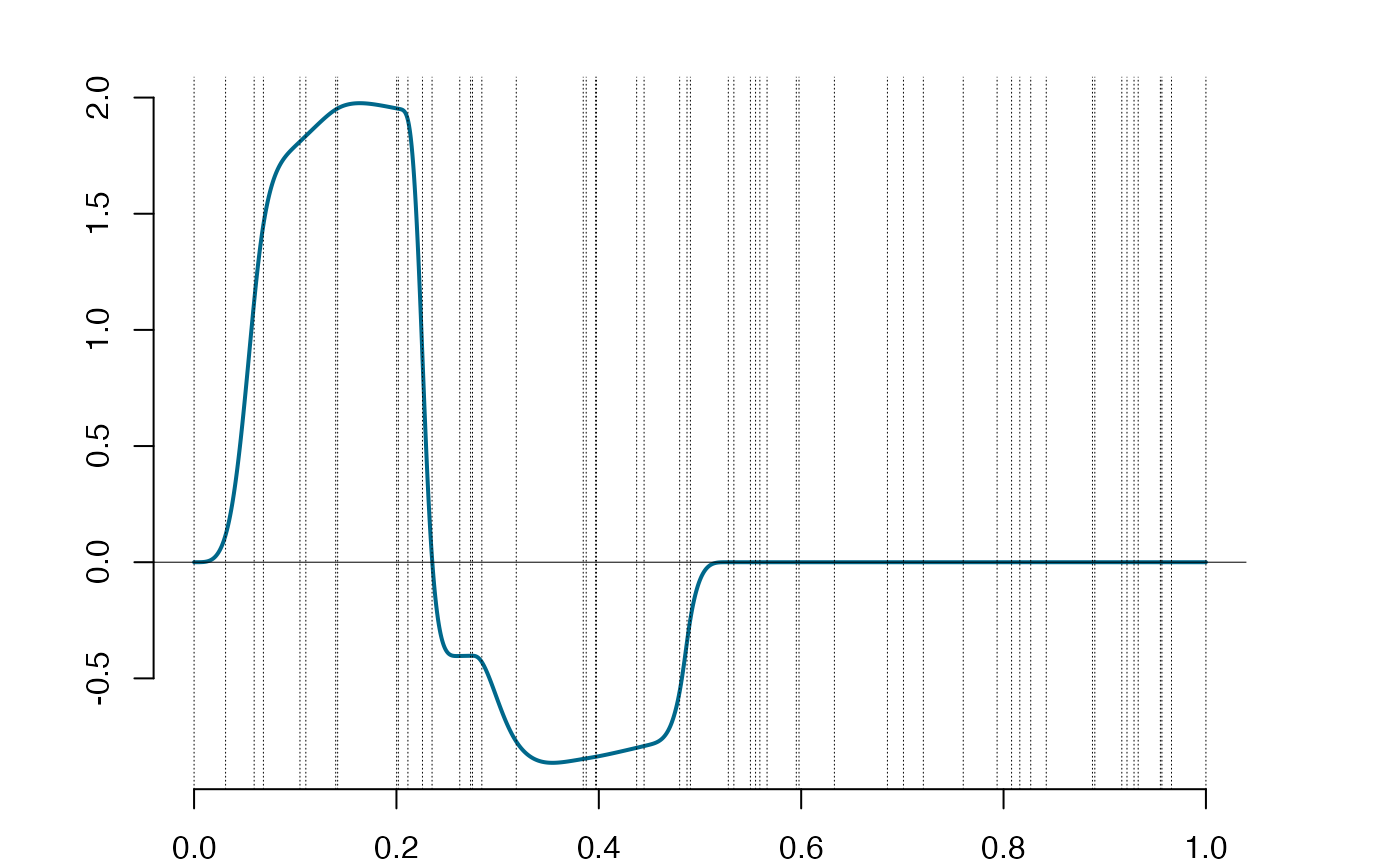s1@supp # lincomb based on support, the full support is reported
#> list()
s2 = lincomb(s, matrix(c(1,1), nrow = 1), reduced = FALSE)
plot(s2)
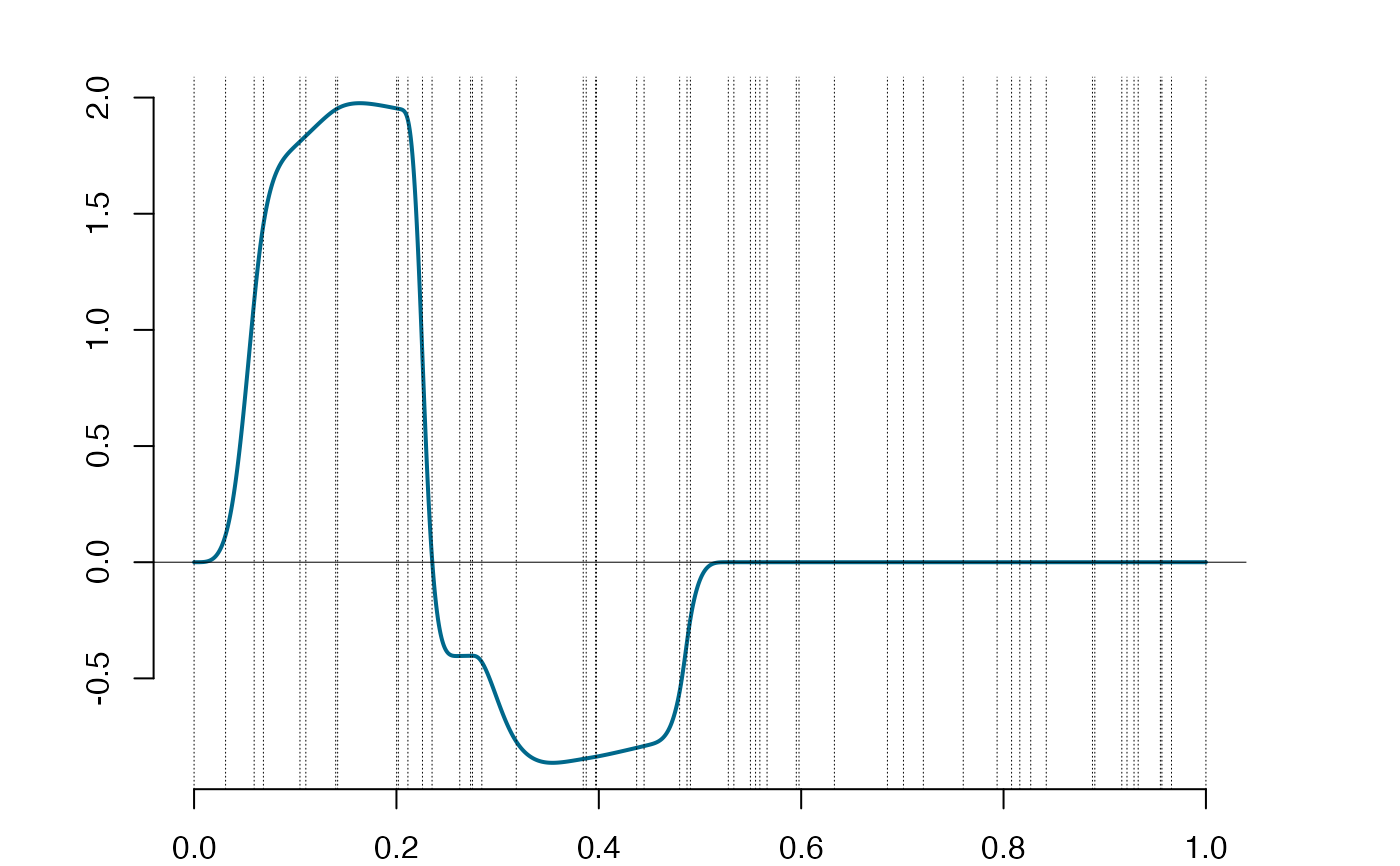s2@supp # lincomb using full der matrix
#> [[1]]
#> [,1] [,2]
#> [1,] 1 28
#>
s3=lincomb(s, matrix(c(1,1), nrow = 1), reduced = FALSE, SuppExtr=FALSE)
s3@supp #the full range is reported as support
#> list()
ES=exsupp(s1@der[[1]]) #correcting the matrix and the support
s1@der[[1]]=ES[[1]]
s1@supp[[1]]=ES[[2]]
plot(s1)
s1@supp[[1]]
#> [,1] [,2]
#> [1,] 1 28