This is a reproducible example of the introduction section of the paper Splinets - Orthogonal Splines for Functional Data Analysis}
Introduction to Splinets
Examples of splines for non-equally spaced knots (first two figures) and equally spaced knots (right). Both individual splines and random spline samples generated around with a use of the implemented random spline generator. Vertical dashed lines in all figures are placed at the locations of the knots.
n=20; k=3 #Number of knots and the order of splines
set.seed(10)
xi=sort(rbeta(n+2,2,5)); xi[1]=0; xi[n+1]=1 #Randomly distributed knots
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1)) #Random matrix of derivatives
spl=construct(xi,k,S) #A spline object with corrected matrix of the derivatives
#>
#> Using method RRM to correct the derivative matrix entries.
#> NOTE: Knots are not in the strictly increasing order, which is required.
#>
#> The knots have been ordered and ties have been removed.
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> Spline 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> The spline 1 'ths highest derivative at the two central knots has been made equal by averaging SLOT 'der'.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.317087 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 5 knots, the first 1 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 5 knots, the first 1 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The matrix derivative is now corrected by method RRM .
plot(spl)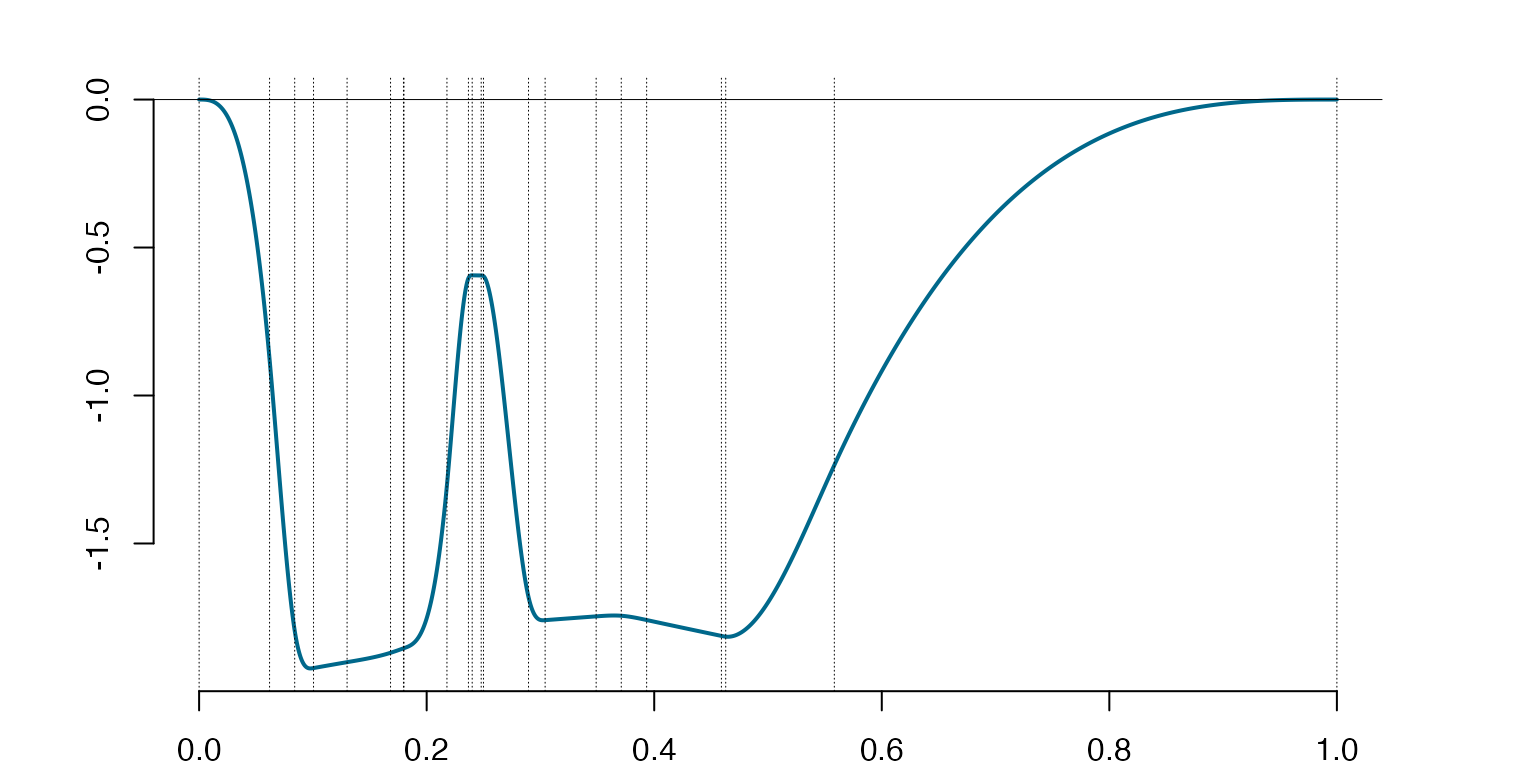
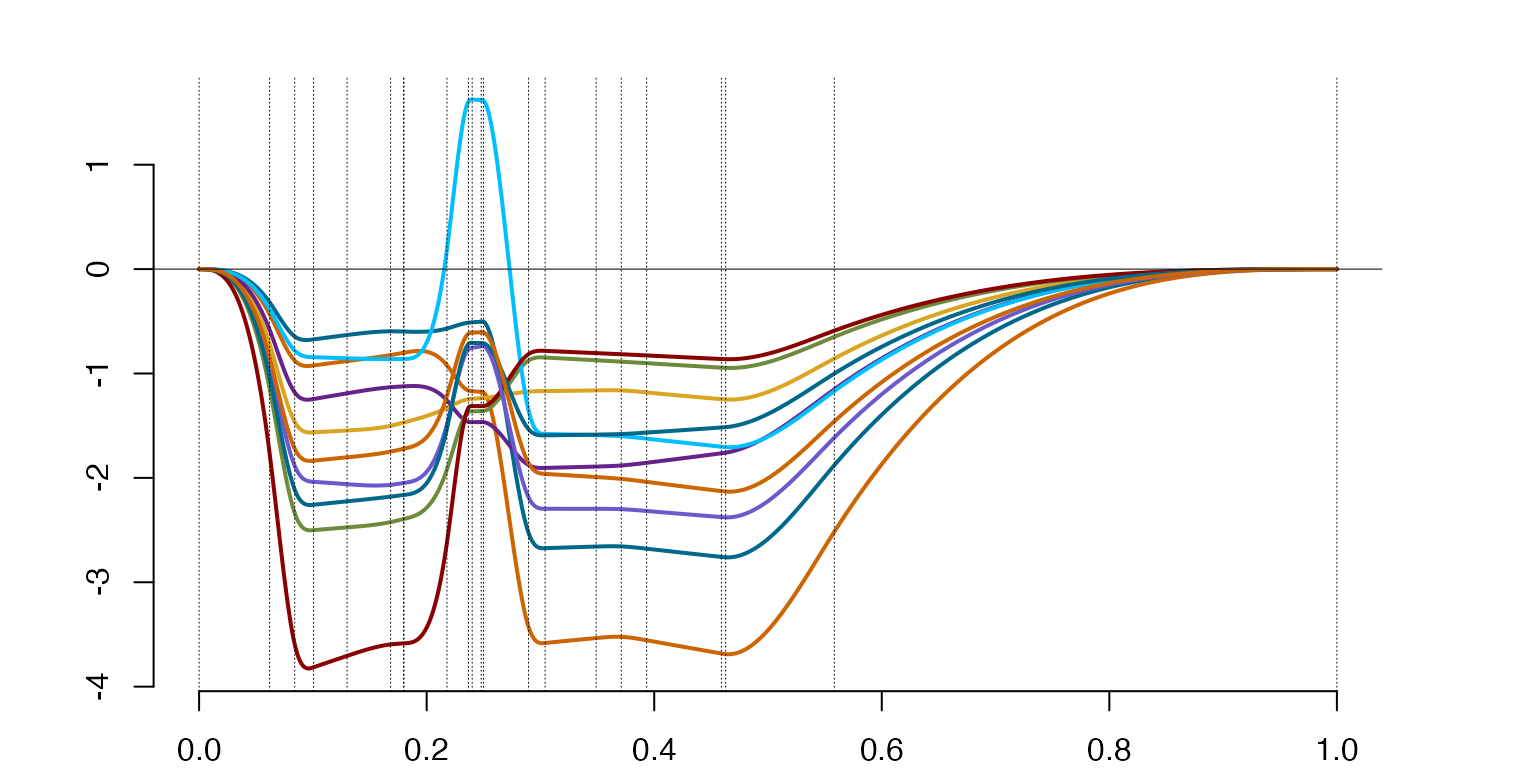
xi2=seq(0,1,by=1/(n+1))
spl2=construct(xi2,k,S) #Another spline object
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> Spline 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 's highest derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 1.326947 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> The matrix derivative is now corrected by method RRM .
plot(spl2)
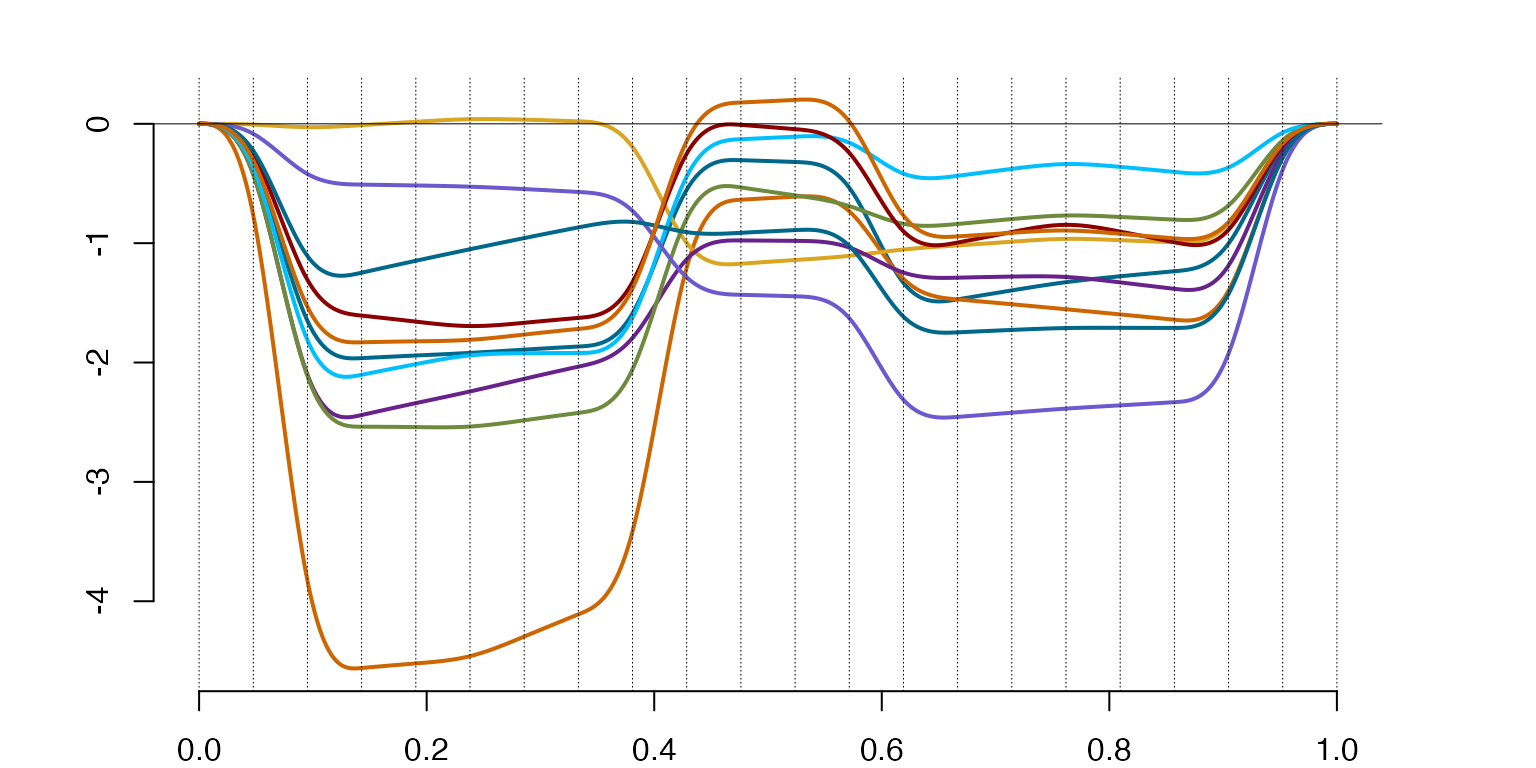
The result is shown in above demonstrate that the knot distribution is fundamental in shaping geometry of functional spaces. The difference in the nature of the two linear functional spaces observed is obvious, as in the first twographs we see more capacity to focus on the localized variability and detail, the capacity that is lacked in splines in the right-hand side graphs.
Orthonormal bases of splines
k=3; N=5 #Order of splines and the number of layers
n=k*2^N-1 #Number of knots
set.seed(2)
xi=cumsum(runif(n+2,min=0.2)) #Random knots
so = splinet(xi, k) #Evaluation of the B-splines and the splinet
plot(so$bs,type='dyadic') #B-splines on the dyadic net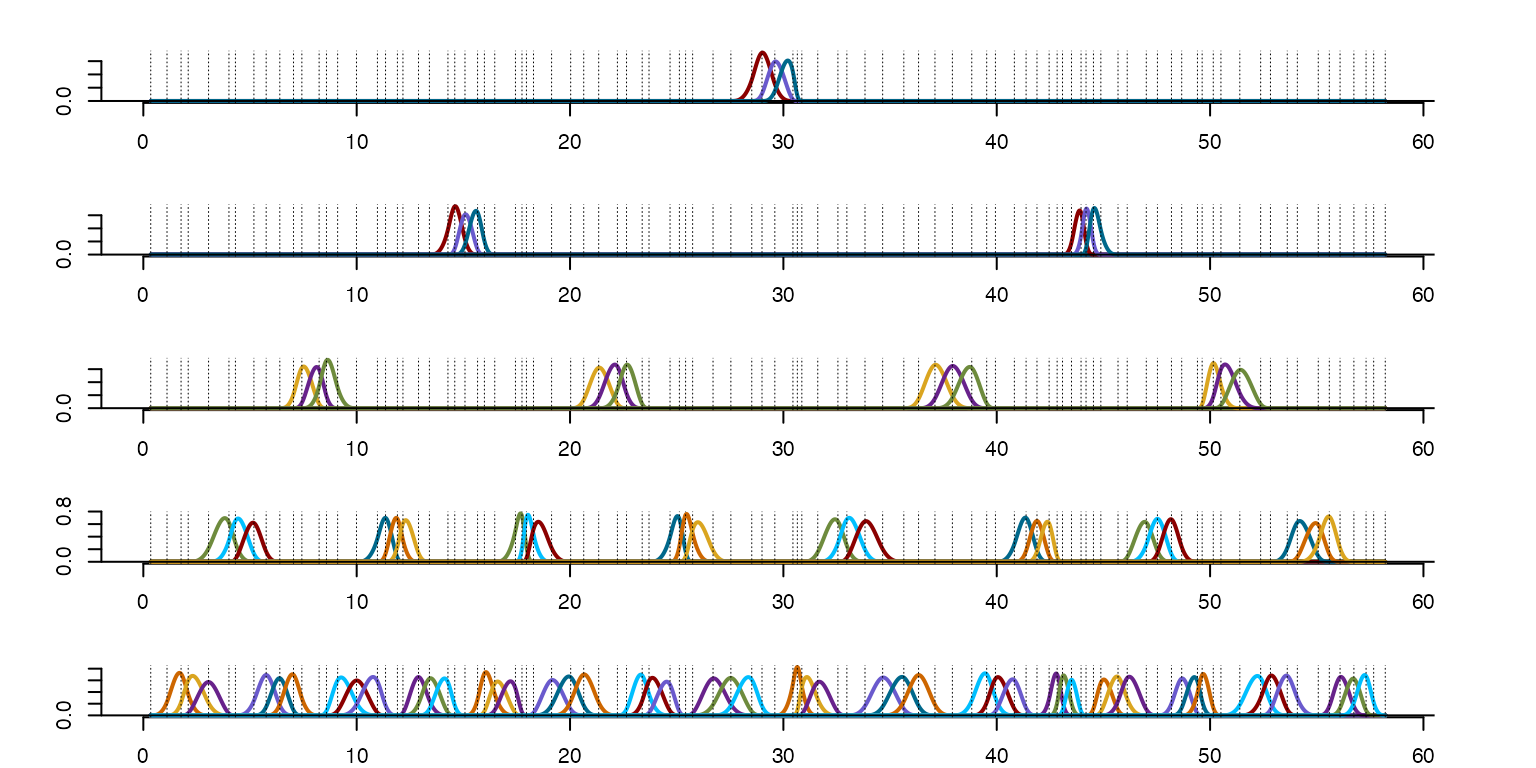
plot(so$os) #Splinet on the dyadic net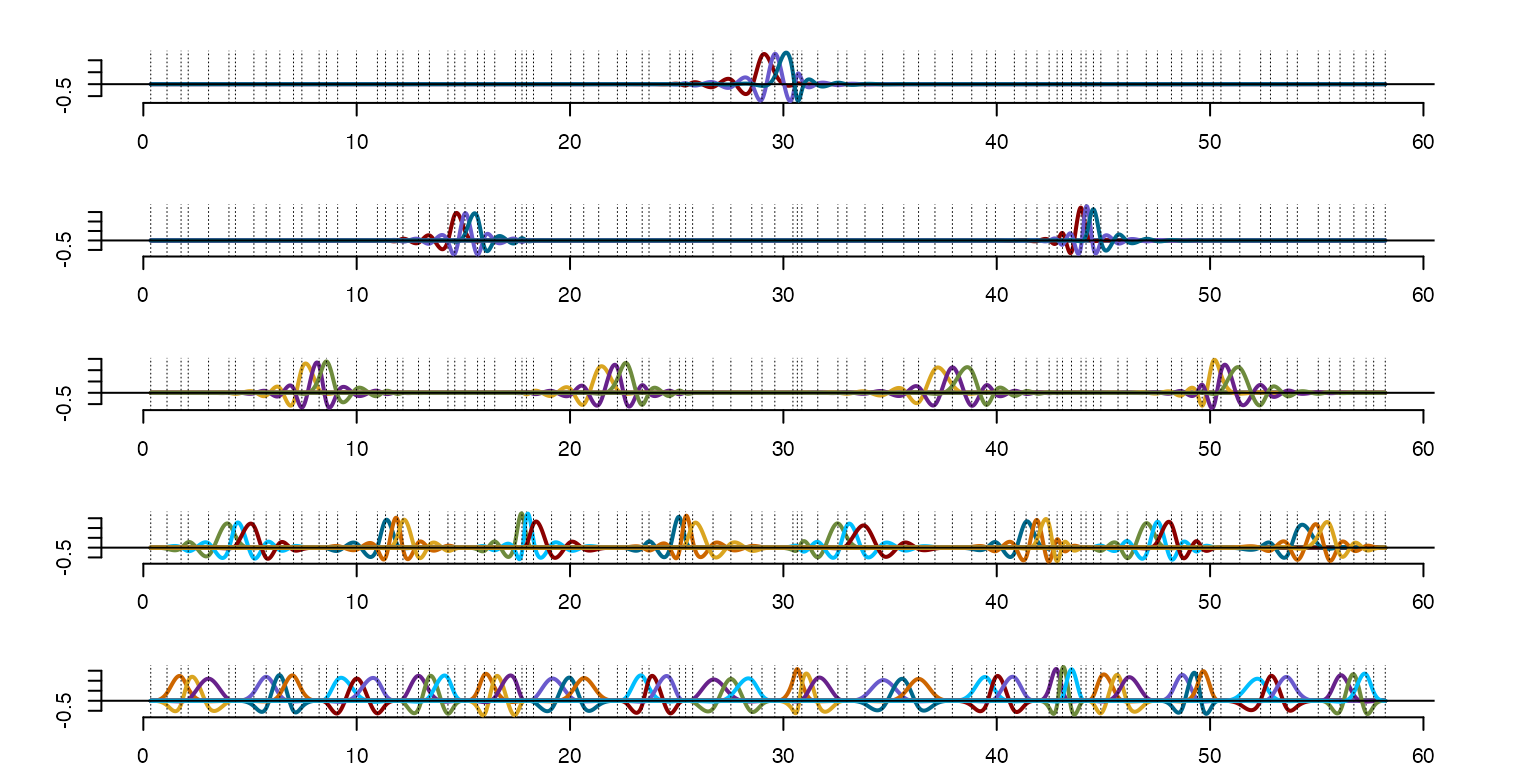
Cubic spline bases presented graphically in the sequential form (top) and on the dyadic net (bottom). The case of , , which is the number of layers in the dyadic structure seen in the figures. The first is the B-spline basis; After is the corresponding splinet.