The B-splines (periodic B-splines) are either given in the input or generated inside the routine. Then, given
the B-splines and the argument type, the routine additionally generates a Splinets-object
representing an orthonormal spline basis obtained from a certain
orthonormalization of the B-splines. Orthonormal spline bases are obtained by one of the following methods:
the Gram-Schmidt method, the two-sided method, and/or the splinet algorithm, which is the default method.
All spline bases are kept in the format of Splinets-objects.
Usage
splinet(
knots = NULL,
smorder = 3,
type = "spnt",
Bsplines = NULL,
periodic = FALSE,
norm = F
)Arguments
- knots
n+2vector, the knots (presented in the increasing order); It is not needed, whenBsplinesargumment is notNULL, in which the case the knots fromBsplinesare inherited.- smorder
integer, the order of the splines, the default is
smorder=3; Again it is inherited from theBsplinesargumment if the latter is notNULL.- type
string, the type of the basis; The following choices are available
'bs'for the unorthogonalized B-splines,'spnt'for the orthogonal splinet (the default),'gsob'for the Gramm-Schmidt (one-sided) O-splines,'twob'for the two-sided O-splines.
- Bsplines
Splinet-object, the basis of the B-splines (if notNULL); When this argument is notNULLthe first two arguments are not needed since they will be inherited fromBsplines.- periodic
logical, a flag to indicate if B-splines will be of periodic type or not;
- norm
logical, a flag to indicate if the output B-splines should be normalized;
Value
Either a list list("bs"=Bsplines) made of a single Splinet-object Bsplines
when type=='bs', which represents the B-splines (the B-splines are normalized or not, depending
on the norm-flag), or a list of two Splinets-objects: list("bs"=Bsplines,"os"=Splinet),
where Bsplines are either computed (in the input Bspline= NULL) or taken from the input Bspline
(this output will be normalized or not depending on the norm-flag),
Splinet is the B-spline orthognalization determined by the input argument type.
Details
The B-spline basis, if not given in
the input, is computed
from the following recurrent (with respect to the smoothness order of the B-splines) formula
$$
B_{l,k}^{\boldsymbol \xi }(x)=
\frac{x- {\xi_{l}}
}{
{\xi_{l+k}}-{\xi_{l}}
}
B_{l,k-1}^{\boldsymbol \xi}(x)
+
\frac{{\xi_{l+1+k}}-x }{ {\xi_{l+1+k}}-{\xi_{l+1}}}
B_{l+1,k-1}^{\boldsymbol \xi}(x), l=0,\dots, n-k.
$$
The dyadic algorithm that is implemented takes into account efficiencies due to the equally space knots
(exhibited in the Toeplitz form of the Gram matrix) only if the problem is fully dyadic, i.e. if the number of
the internal knots is smorder*2^N-1, for some integer N. To utilize this efficiency it may be advantageous,
for a large number of equally spaced knots, to choose them so that their number follows the fully dyadic form.
An additional advantage of the dyadic form is the complete symmetry at all levels of the support. The algorithm works with
both zero boundary splines and periodic splines.
References
Liu, X., Nassar, H., Podg\(\mbox{\'o}\)rski, K. "Dyadic diagonalization of positive definite band matrices and efficient B-spline orthogonalization." Journal of Computational and Applied Mathematics (2022) <https://doi.org/10.1016/j.cam.2022.114444>.
Podg\(\mbox{\'o}\)rski, K. (2021)
"Splinets – splines through the Taylor expansion, their support sets and orthogonal bases." <arXiv:2102.00733>.
Nassar, H., Podg\(\mbox{\'o}\)rski, K. (2023) "Splinets 1.5.0 – Periodic Splinets." <arXiv:2302.07552>
See also
project for projecting into the functional spaces spanned by the spline bases;
lincomb for evaluation of a linear combination of splines;
seq2dyad for building the dyadic structure for a splinet of a given smoothness order;
plot,Splinets-method for visualisation of splinets;
Examples
#--------------------------------------#
#----Splinet, equally spaced knots-----#
#--------------------------------------#
k=2 # order
n_knots = 5 # number of knots
xi = seq(0, 1, length.out = n_knots)
so = splinet(xi, k)
plot(so$bs) #Plotting B-splines
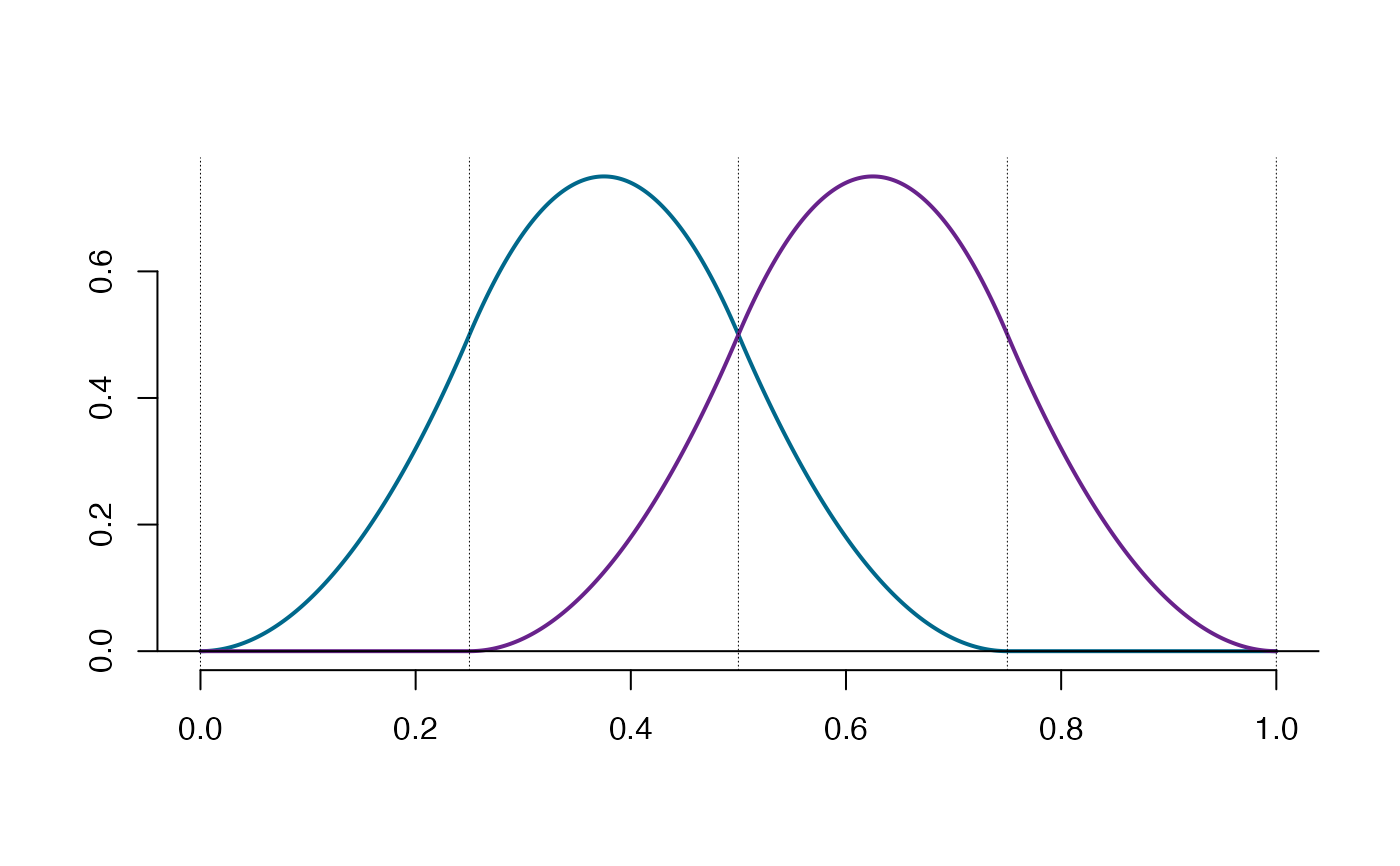plot(so$os) #Plotting Splinet
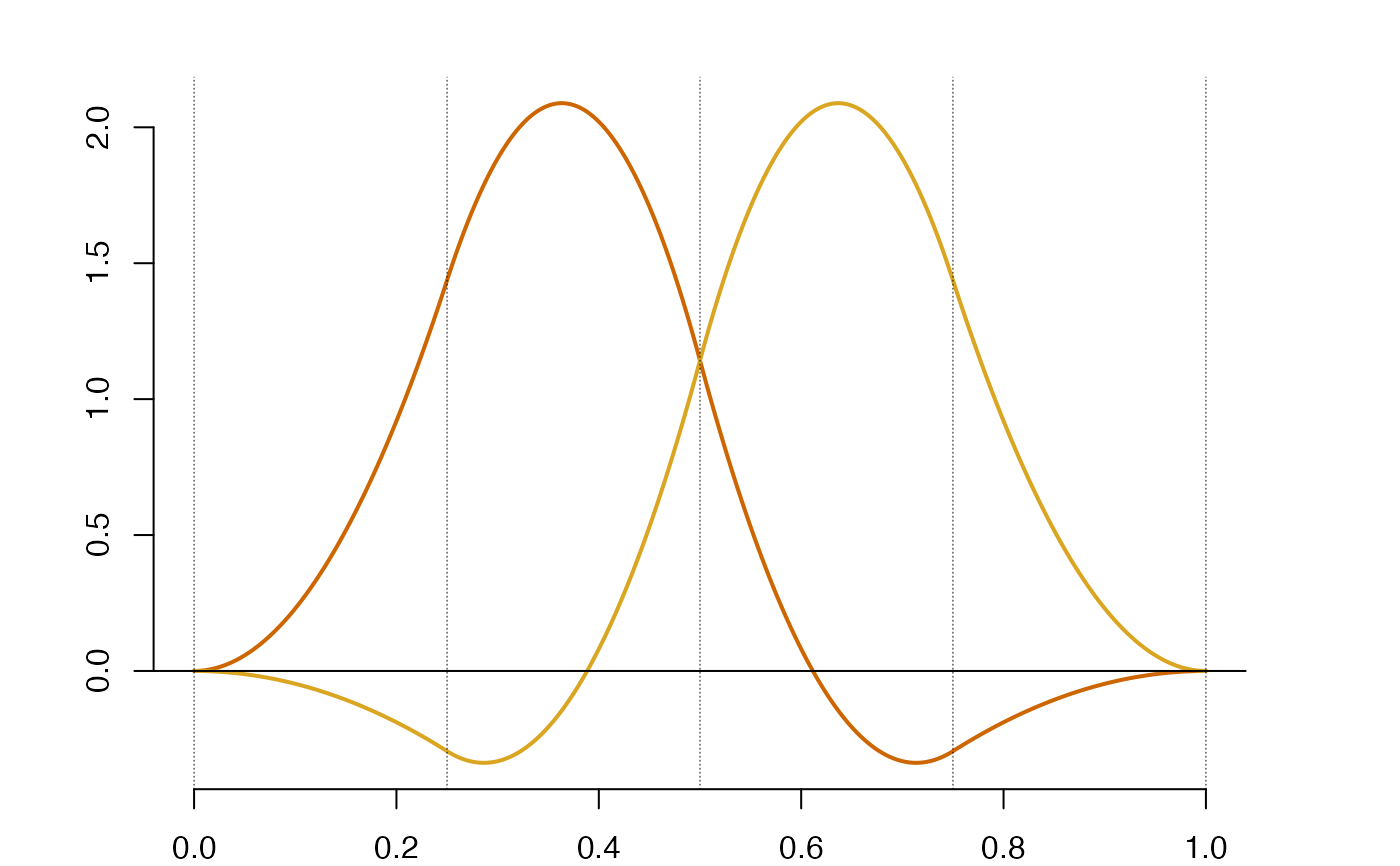#Verifying the orthogonalization
gm = gramian(so$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1
sum(gm - diag(diag(gm)))
#> [1] -1.319476e-15
#An example of the dyadic structure with equally spaced knots
k=3
N=3
n_knots=2^N*k-1 #the number of internal knots for the dyadic case
xi = seq(0, 1, length.out = n_knots+2)
so = splinet(xi)
plot(so$bs,type="simple",vknots=FALSE,lwd=3) #Plotting B-splines in a single simple plot
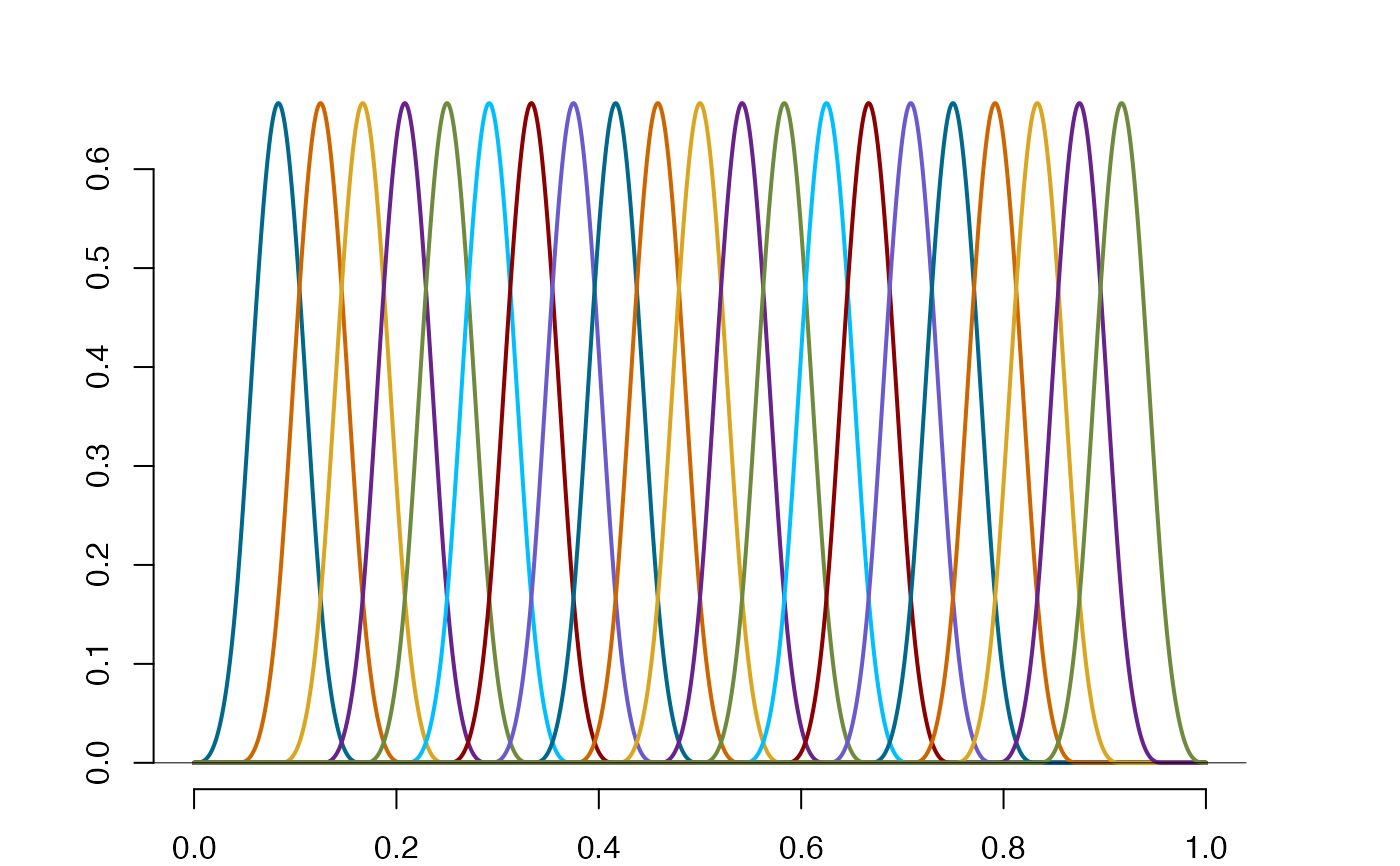plot(so$os,type="simple",vknots=FALSE,lwd=3)
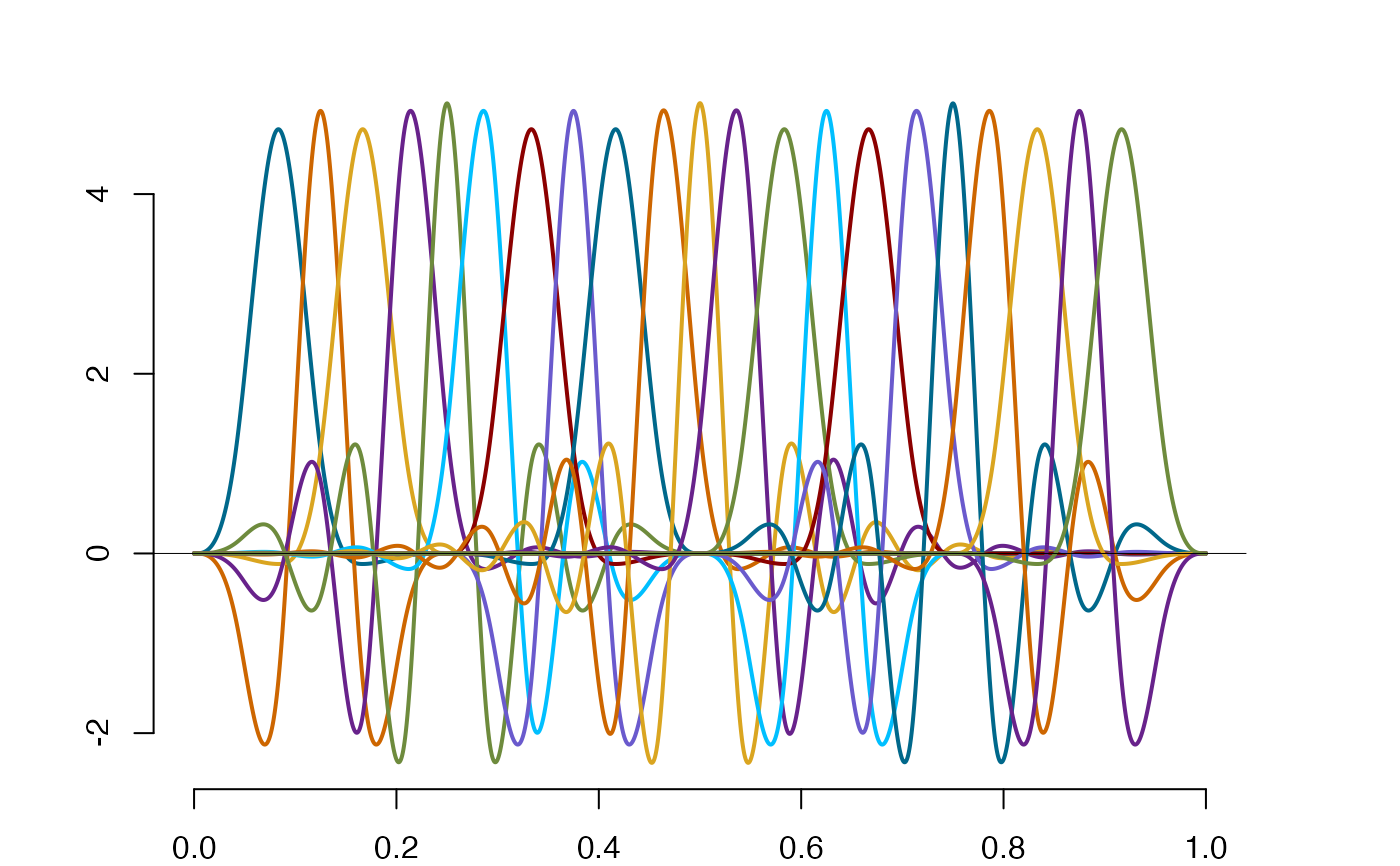plot(so$os,lwd=3,mrgn=2) #Plotting the splinet on the dyadic net of support intervals
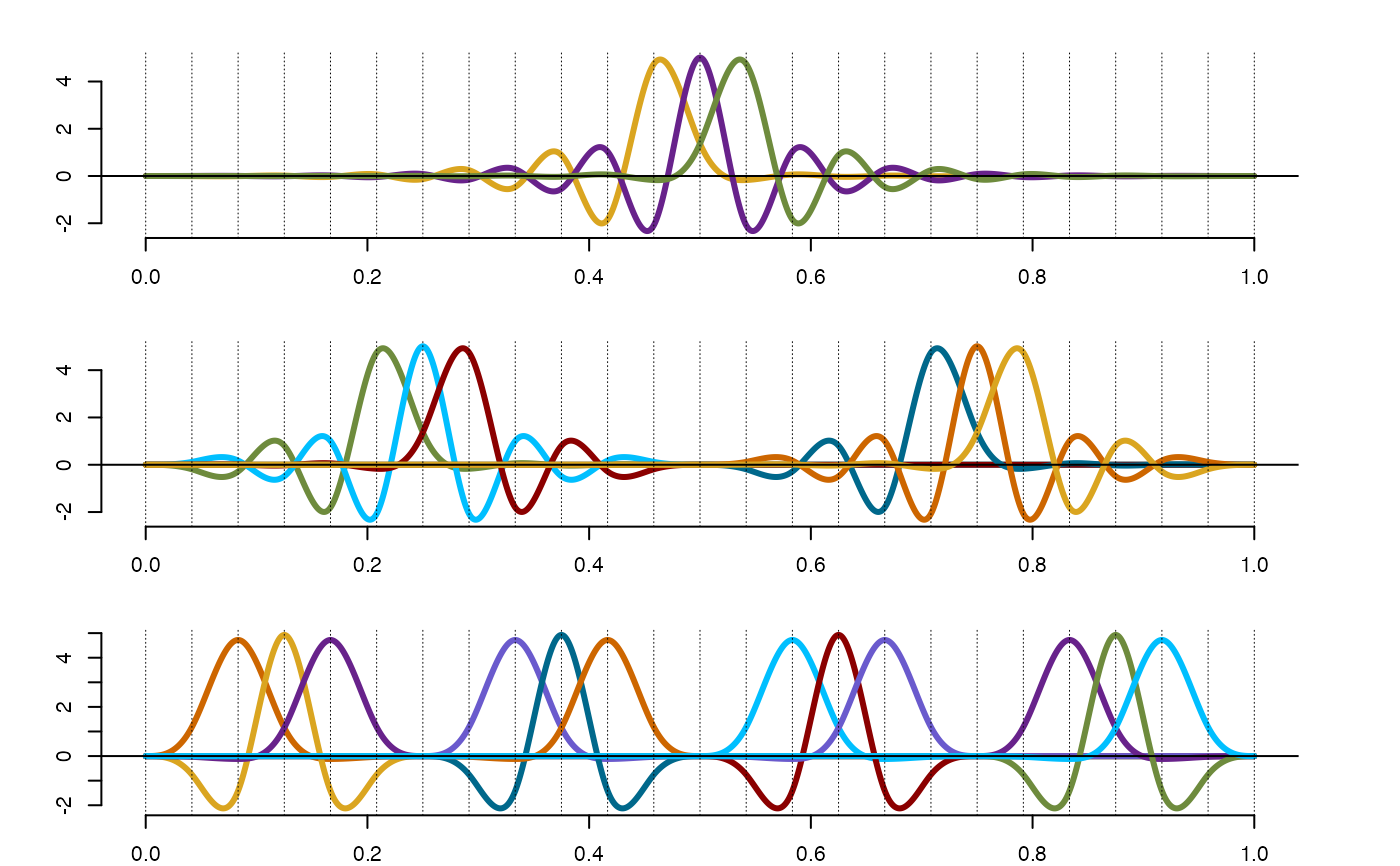so=splinet(xi, Bsplines=so$bs, type='gsob') #Obtaining the Gram-Schmidt orthogonalization
plot(so$os,type="simple",vknots=FALSE) #Without computing B-splines again
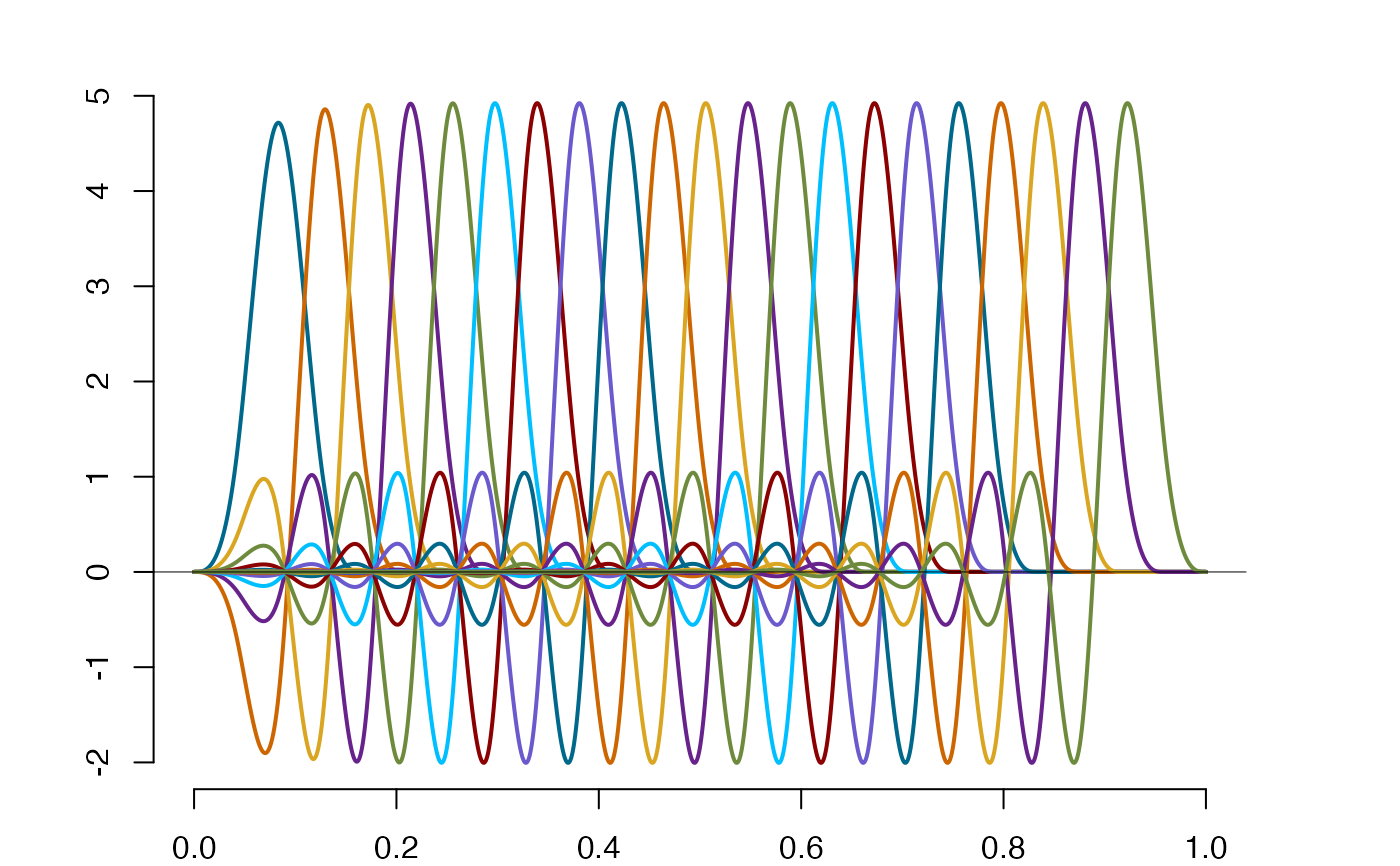so=splinet(xi, Bsplines=so$bs, type='twob') #Obtaining the symmetrize orthogonalization
plot(so$os,type="simple",vknots=FALSE)
#-------------------------------------#
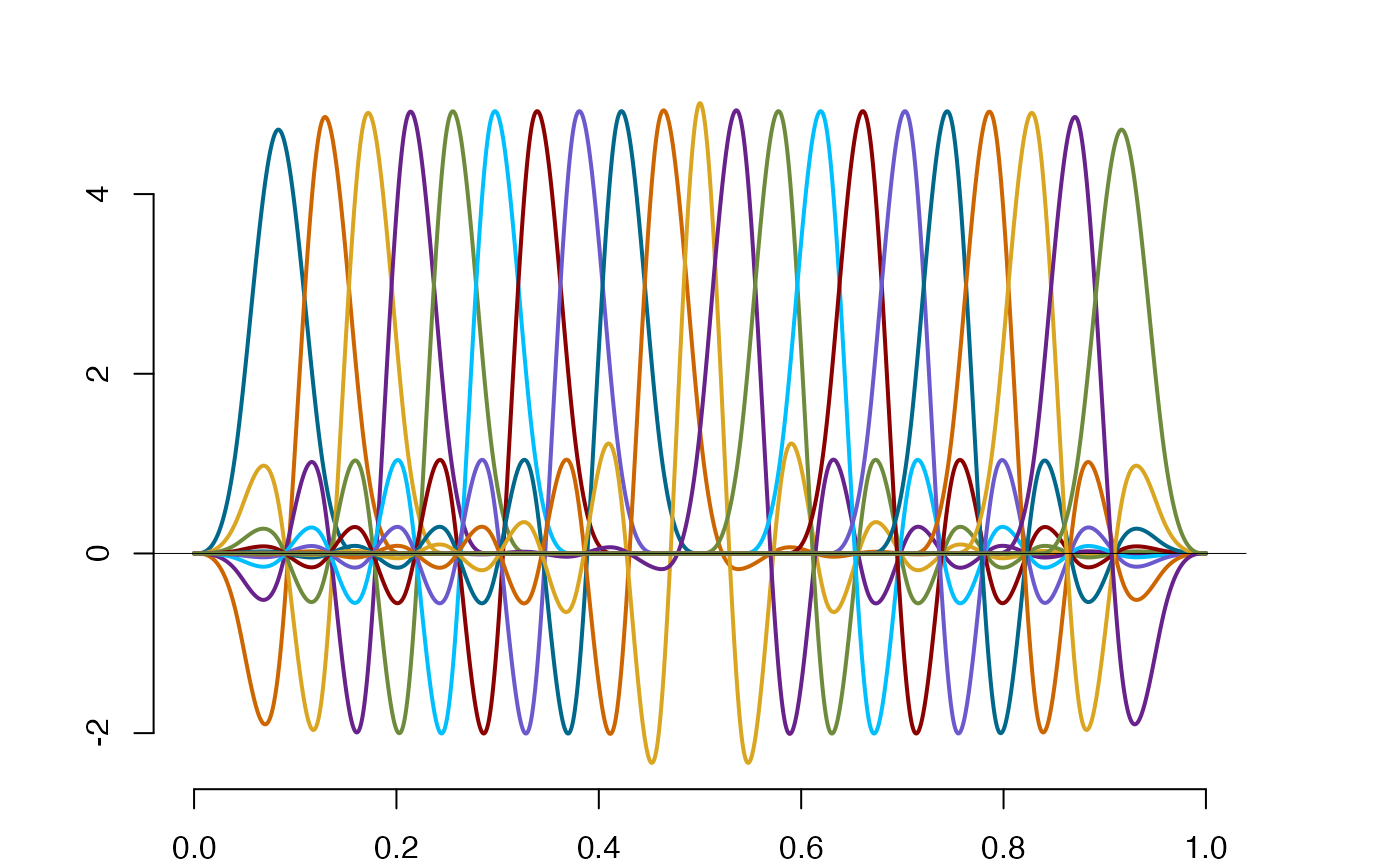#---Splinet, unequally spaced knots---#
#-------------------------------------#
n_knots=25
xi = c(0, sort(runif(n_knots)), 1)
sone = splinet(xi, k)
plot(sone$bs, type='dyadic') #Plotting B-splines
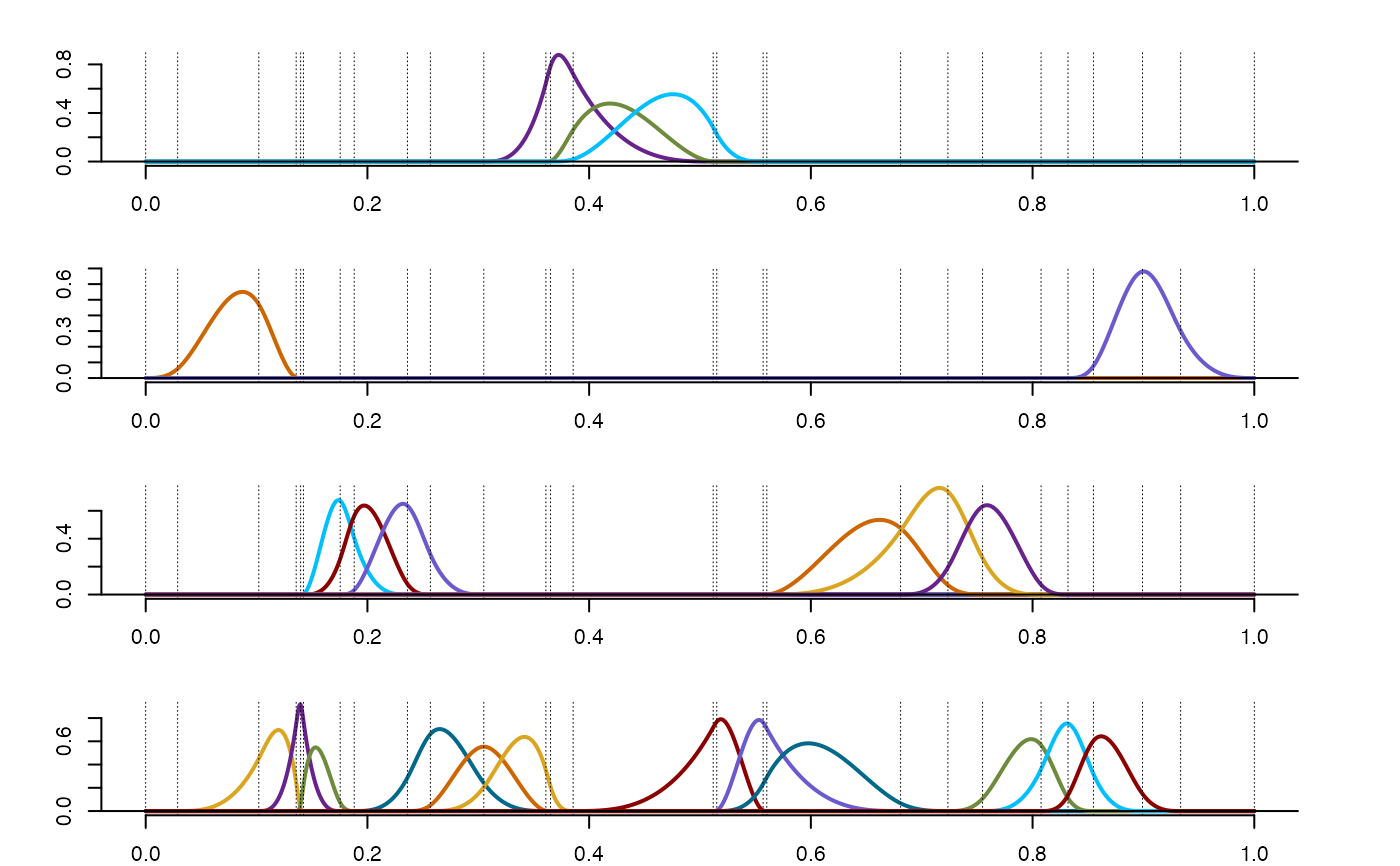plot(sone$os) #Plotting Splinet
#Verifying the orthogonalization
gm = gramian(sone$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -2.164443e-13
#------------------------------------------#
#---Dyadic splinet, equally spaced knots---#
#------------------------------------------#
k = 2 # order
N = 3 # support level
n_so = k*(2^N-1) # number of splines in a dyadic structure with N and k
n_knots = n_so + k + 1 # number of knots
xi = seq(0, 1, length.out = n_knots)
sodyeq = splinet(xi, k)
plot(sodyeq$bs) #Plotting B-splines
plot(sodyeq$os) #Plotting Splinet
#Verifying the orthogonalization
gm = gramian(sodyeq$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -1.52321e-14
#--------------------------------------------#
#---Dyadic splinet, unequally spaced knots---#
#--------------------------------------------#
xi = c(0, sort(runif(n_knots)), 1)
sody = splinet(xi, k)
plot(sody$bs) #Plotting B-splines
plot(sody$os) #Plotting Splinet
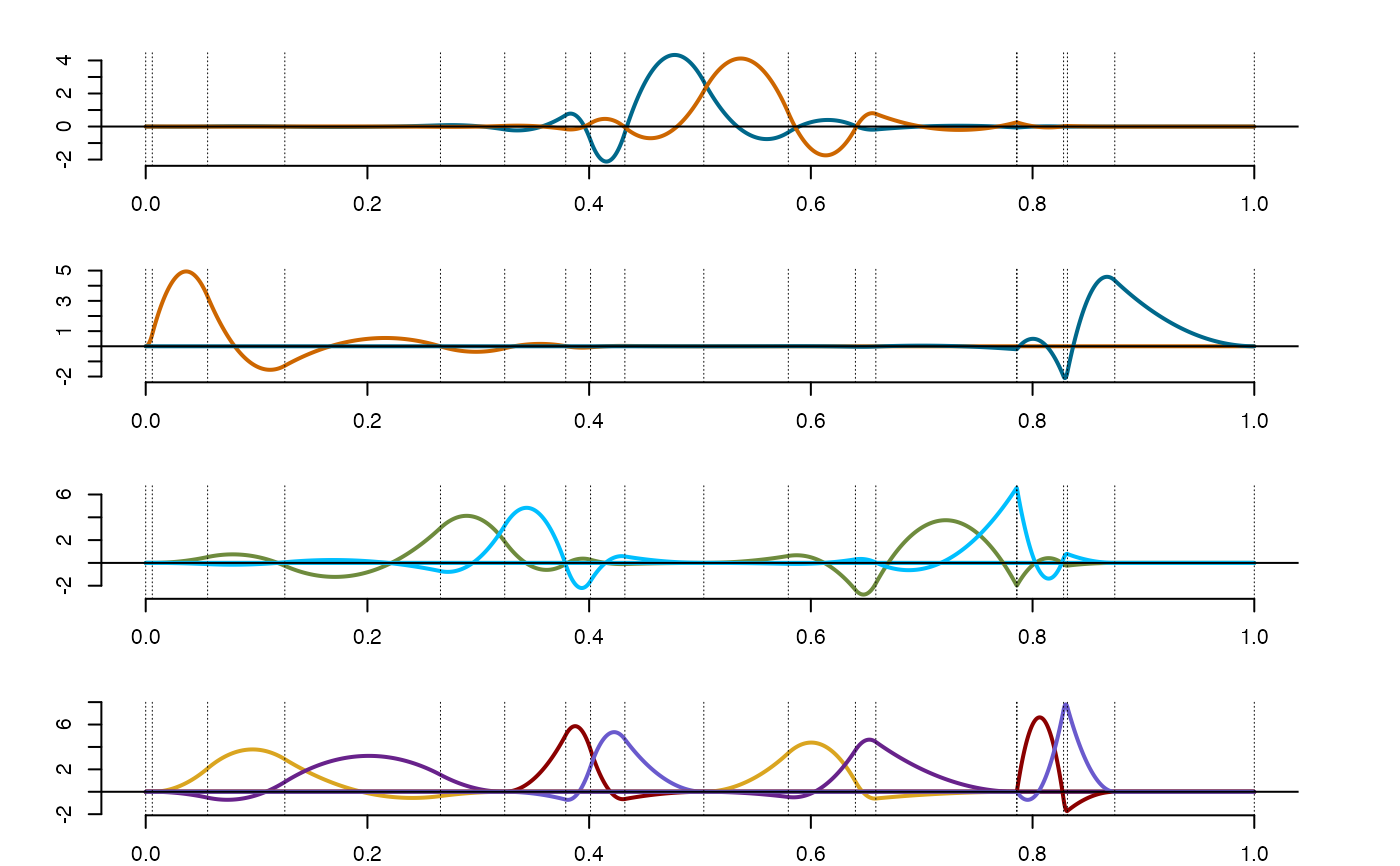#Verifying the orthogonalization
gm = gramian(sody$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -1.275806e-14
#-----------------------------------------#
#---Bspline basis, equally spaced knots---#
#-----------------------------------------#
n = 15
xi = seq(0,1,length.out = n+2)
order = 2
bs = splinet(xi, order, type = 'bs')
plot(bs$bs)
#---------------------------------------------#
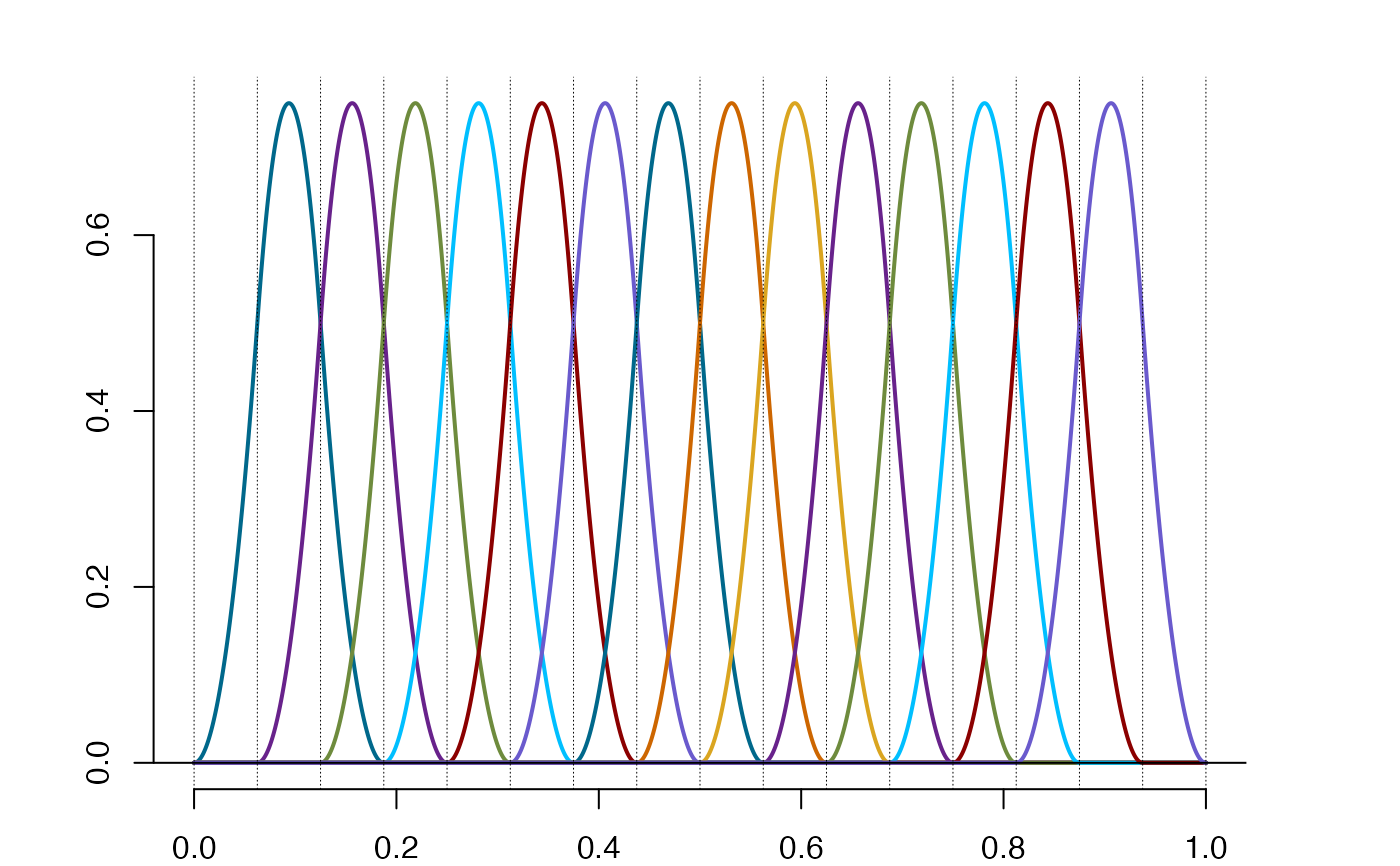#---Bspline basis, non-equally spaced knots---#
#---------------------------------------------#
n = 6
xi = c(0,sort(runif(n)),1)
order = 3
so = splinet(xi, order, type = 'bs') #unnormalized version
plot(so$bs)
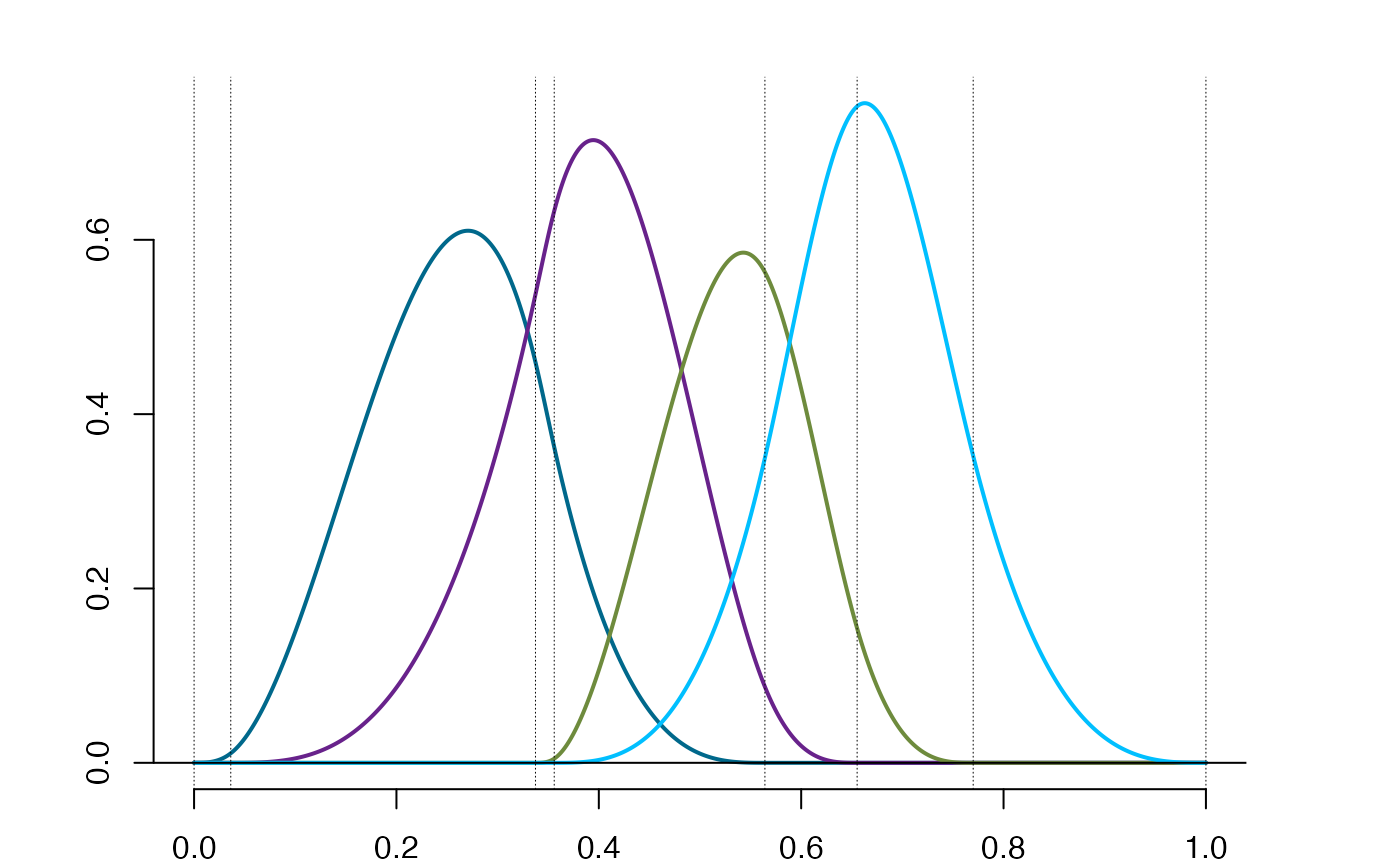so1 = splinet(type='bs',Bsplines=so$bs,norm=TRUE) #normalized version
plot(so1$bs)
#-------------------------------------------------#
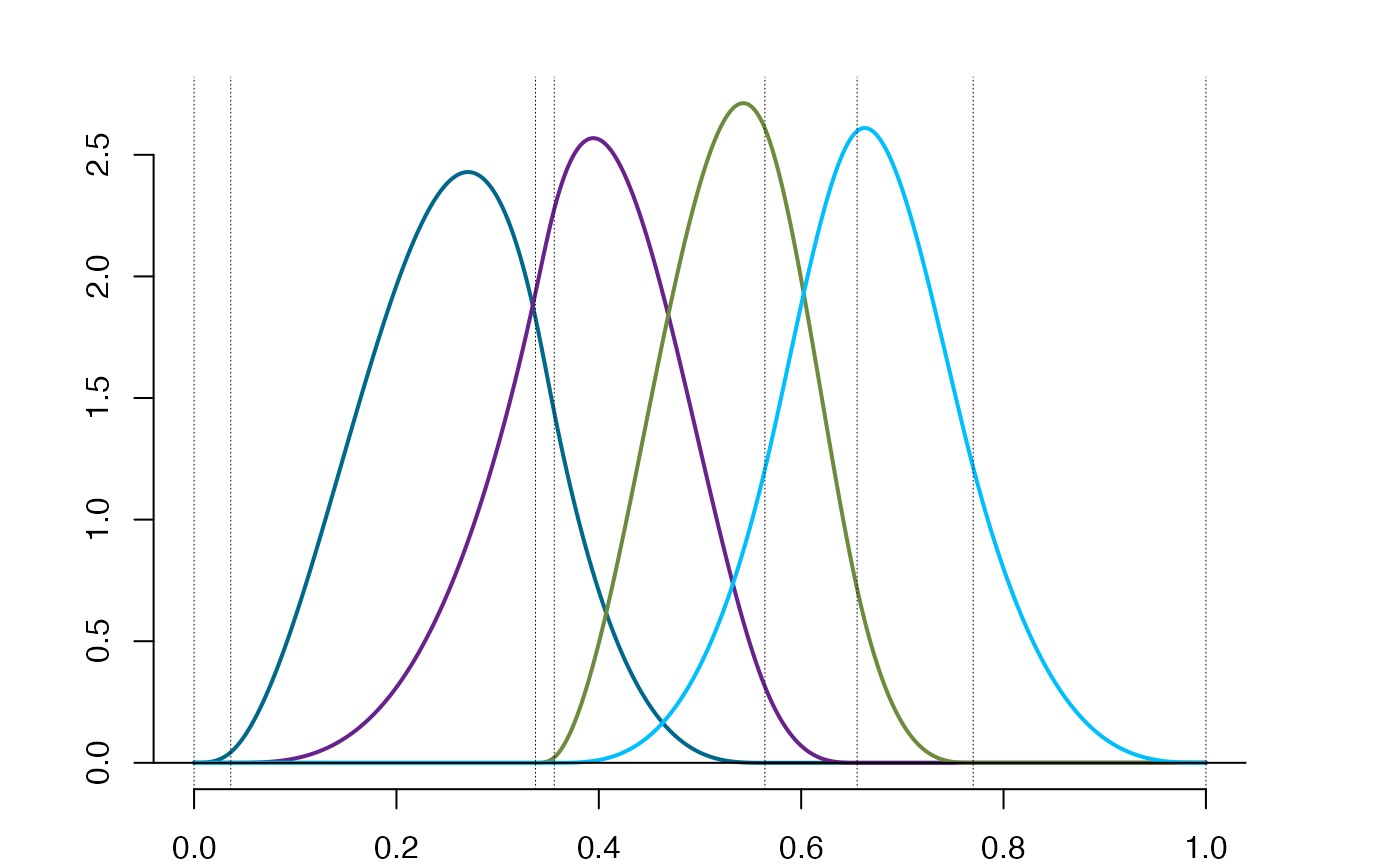#---Gram-Schmidt osplines, equally spaced knots---#
#-------------------------------------------------#
so = splinet(xi, order, type = 'gsob')
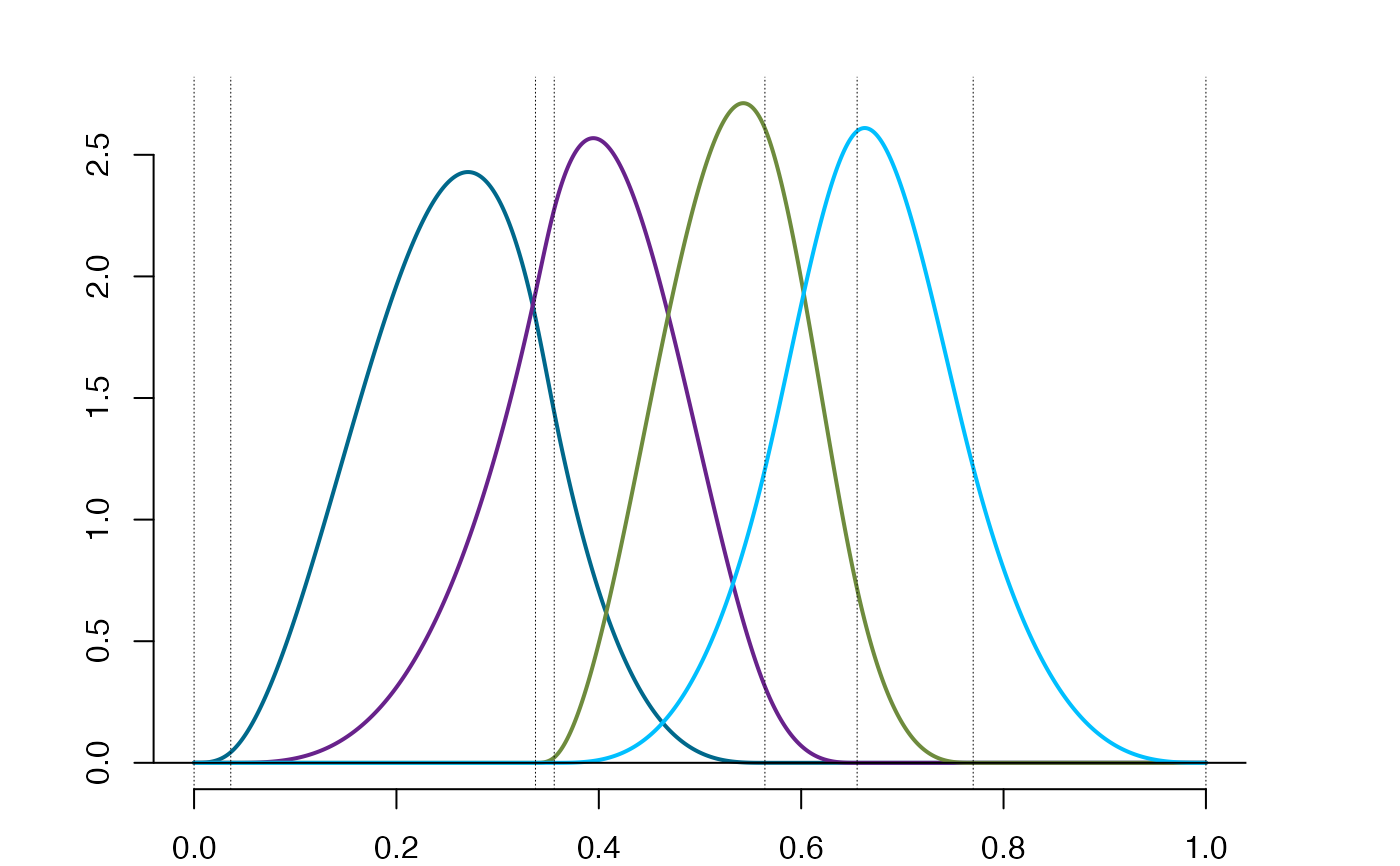
plot(so$bs)
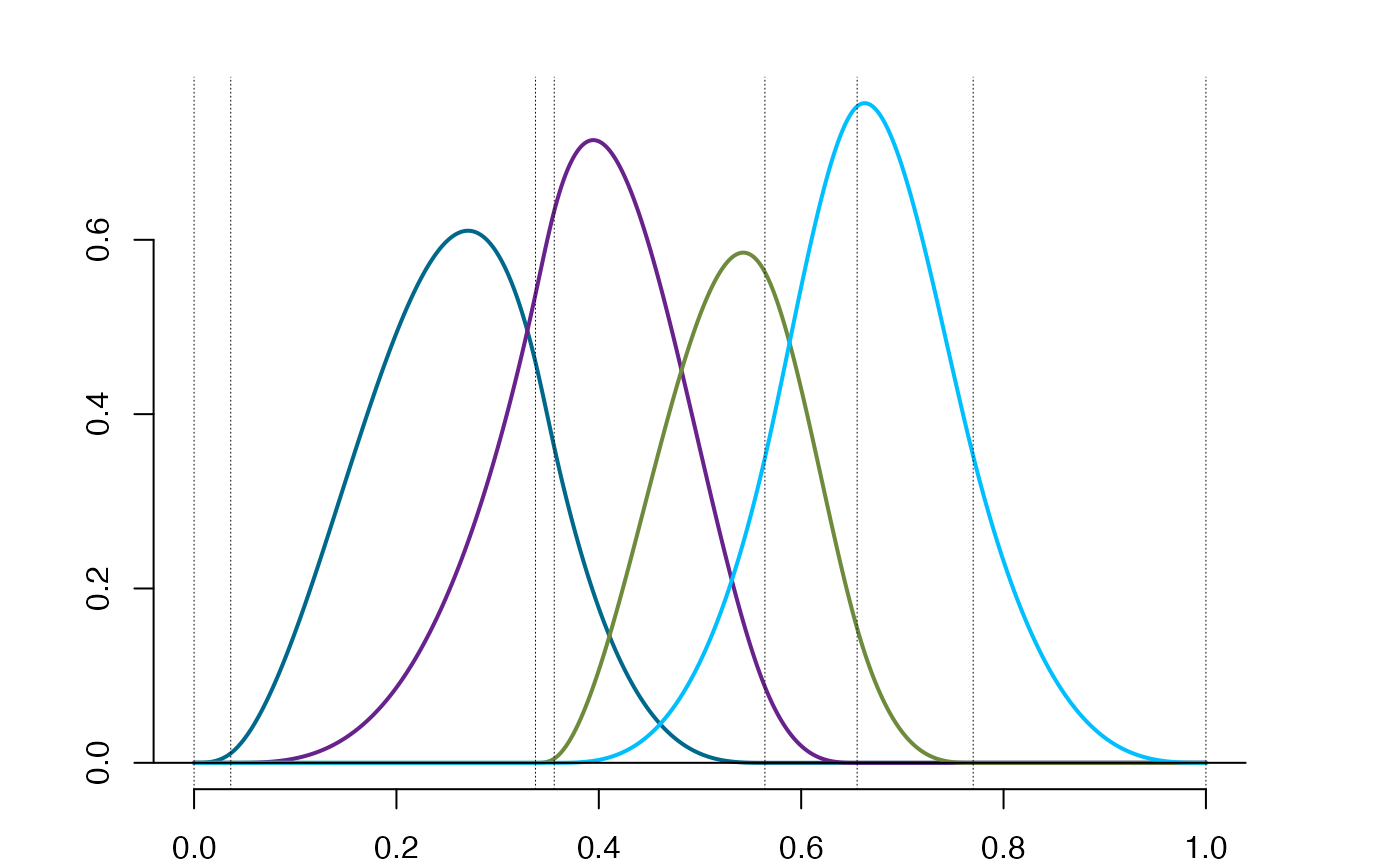plot(so$os)
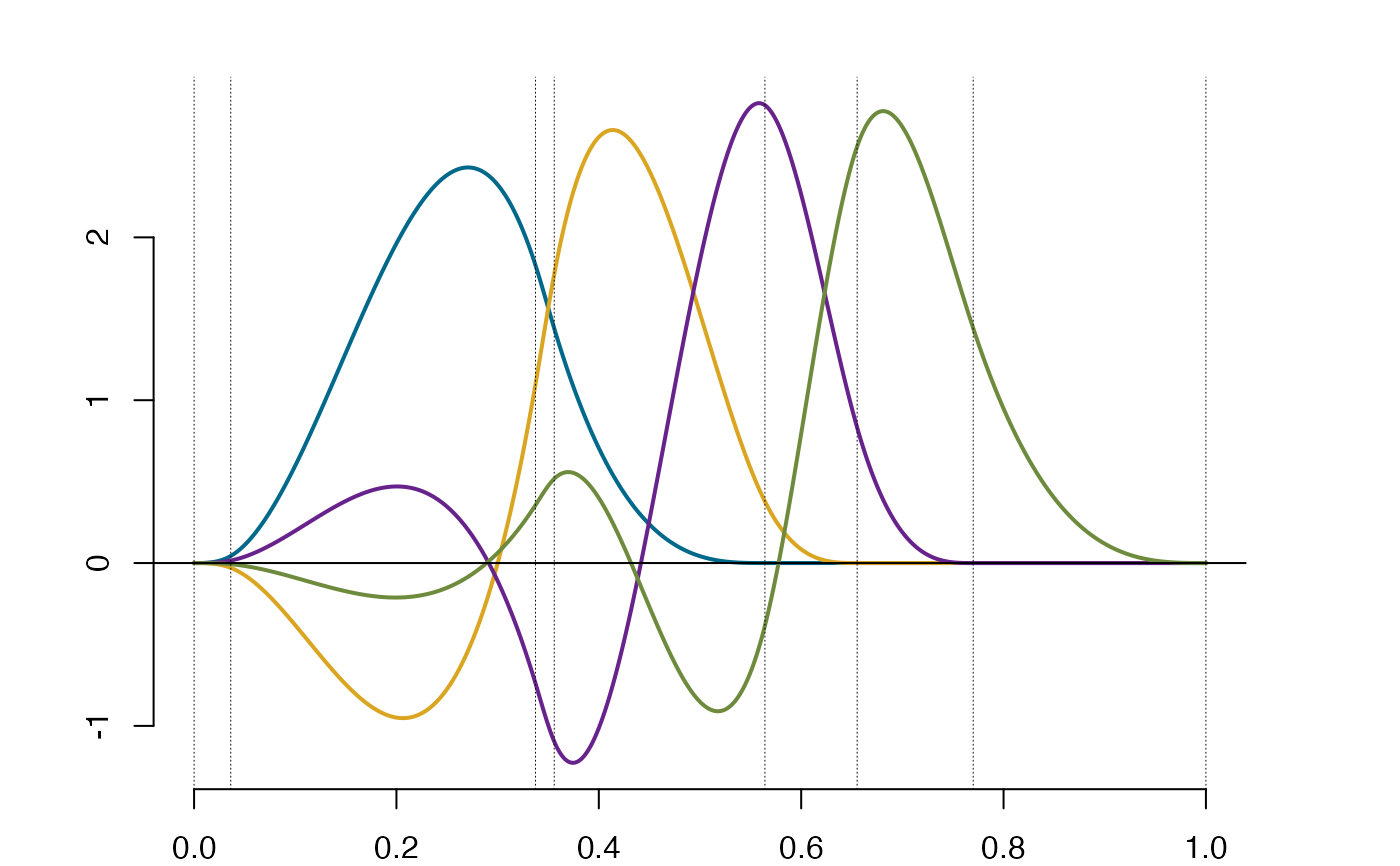
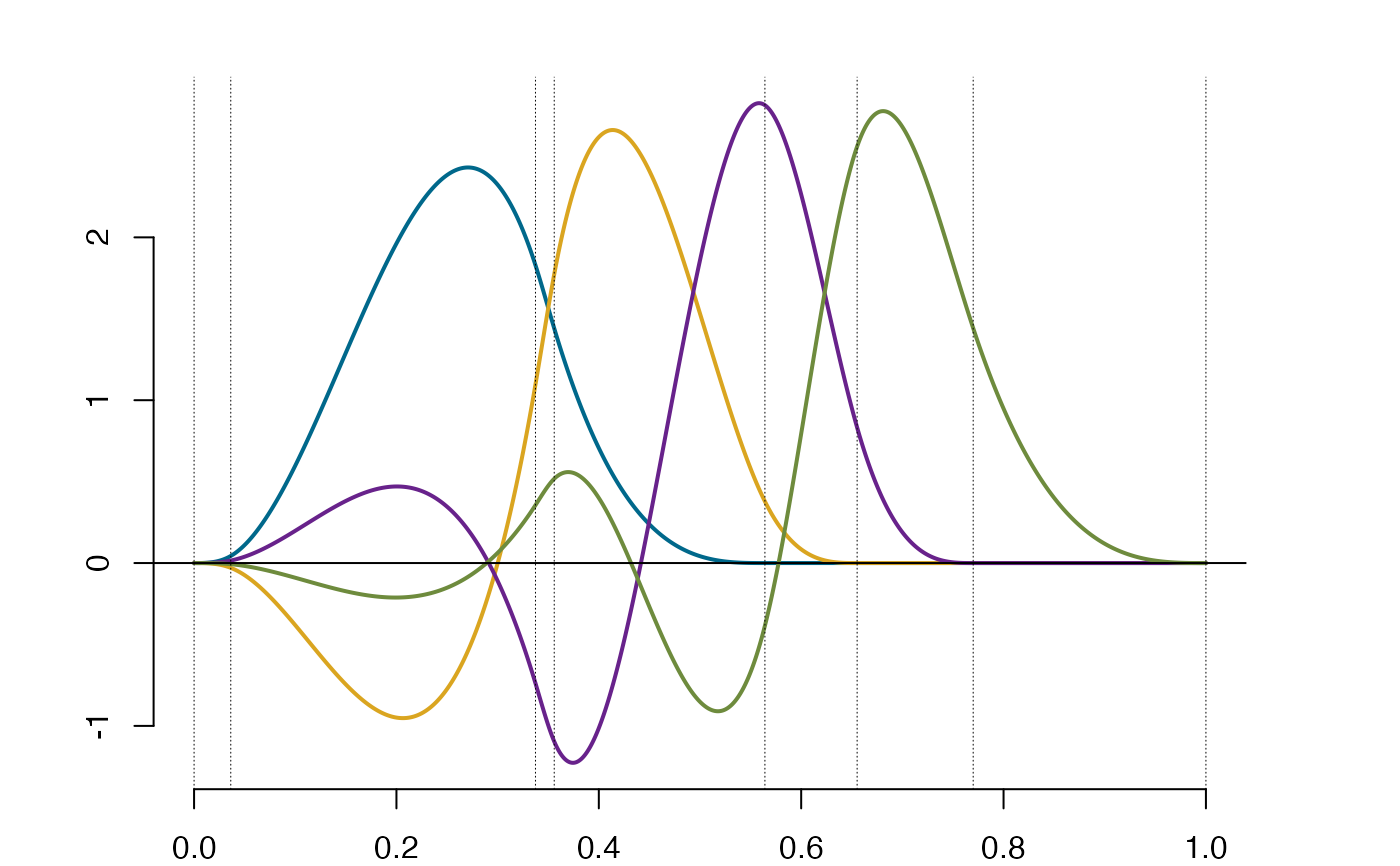#Using the previously generated B-splines and normalizing them
so1 = splinet(Bsplines=so$bs, type = "gsob",norm=TRUE)
plot(so1$bs) #normalized B-splines
plot(so1$os) #the one sided osplines
gm = gramian(so1$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1
sum(gm - diag(diag(gm))) #verification of the orghonoalization of the matrix
#> [1] -2.520335e-15
#-----------------------------------------------------#
#---Gram-Schmidt osplines, non-equally spaced knots---#
#-----------------------------------------------------#
so = splinet(Bsplines=sody$bs, type = 'gsob') #previously genereted Bsplines
plot(so$bs)
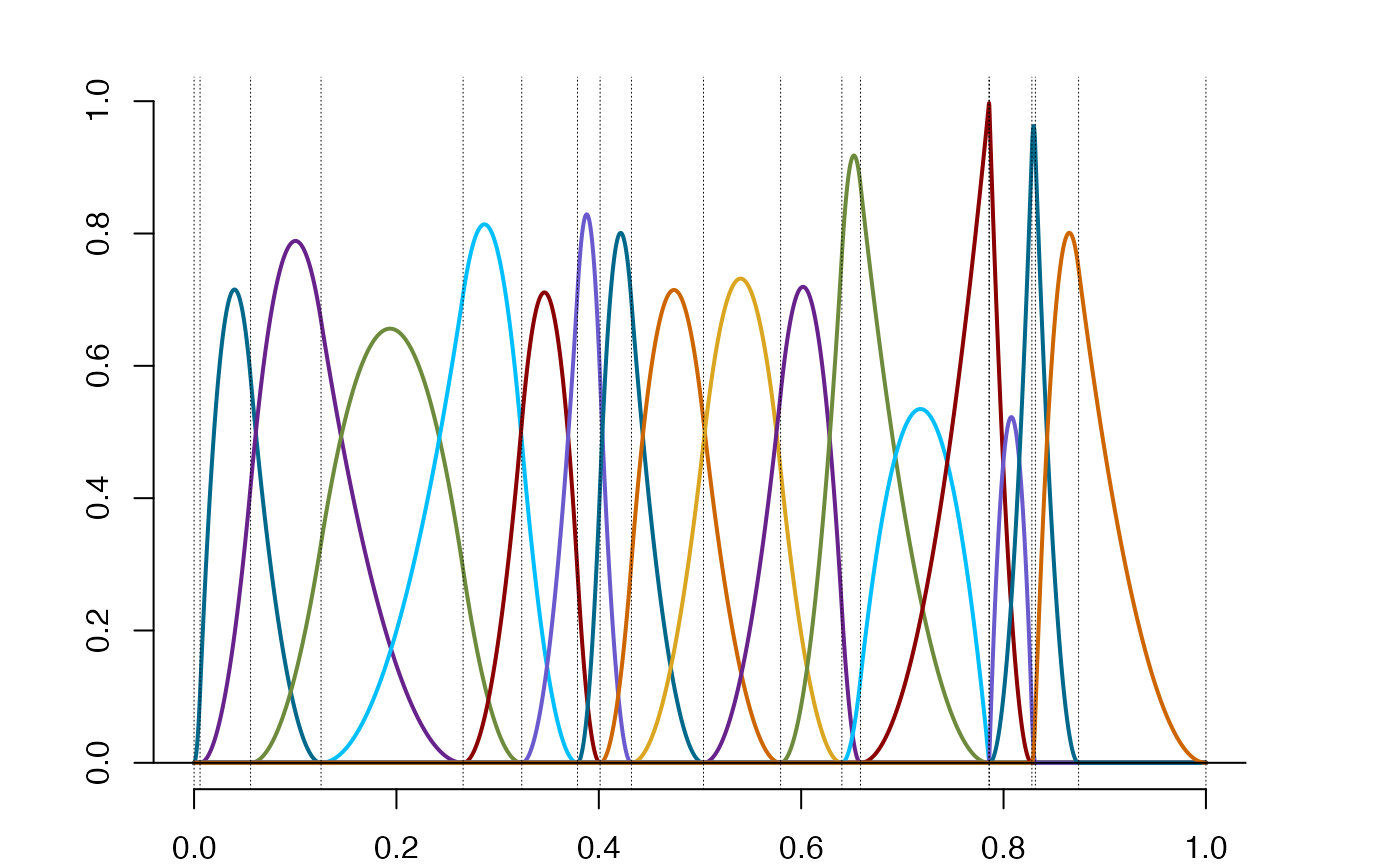plot(so$os)
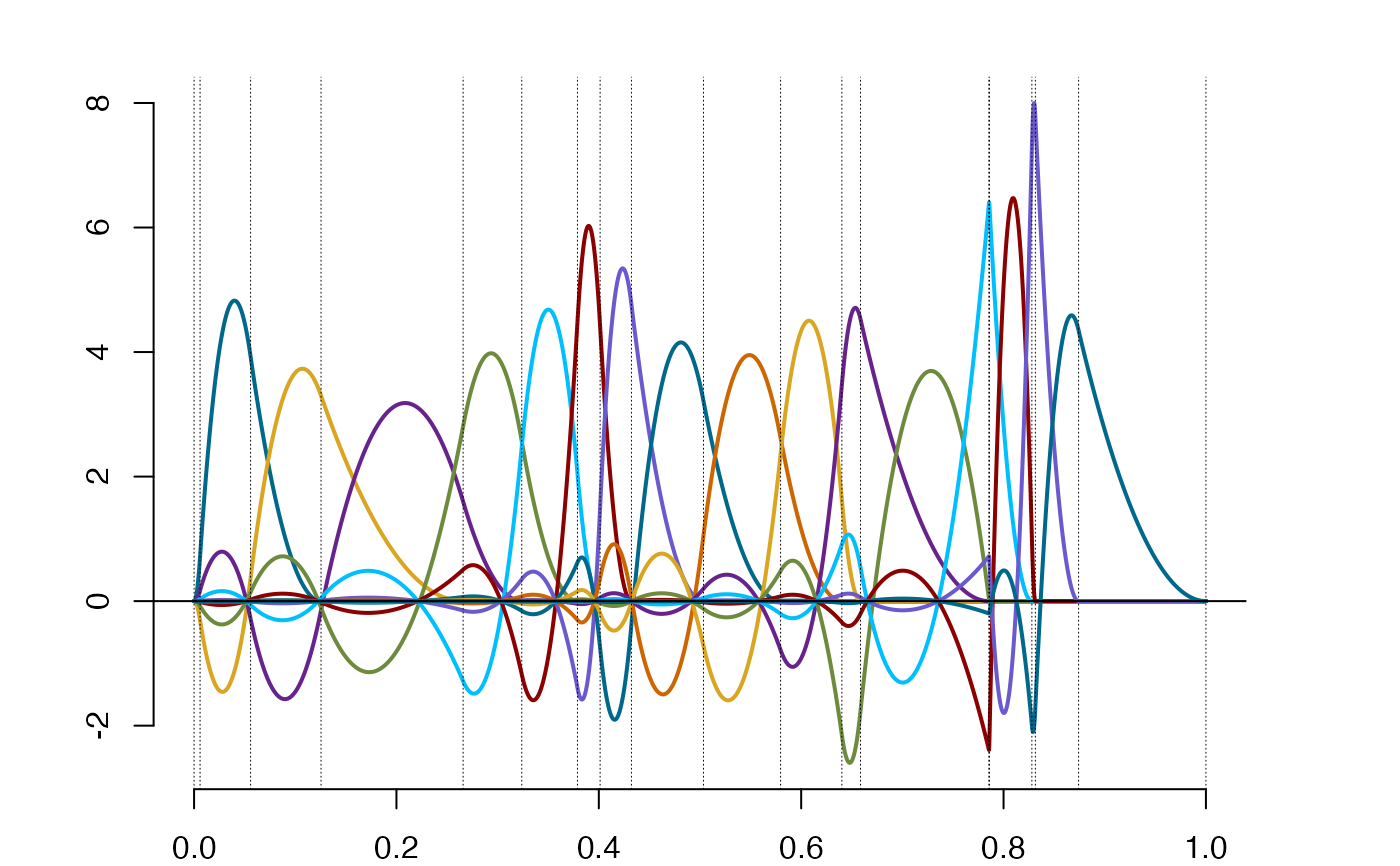gm = gramian(so$os)
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -1.611008e-14
#---------------------------------------------#
#---Twosided osplines, equally spaced knots---#
#---------------------------------------------#
so = splinet(Bsplines=bs$bs, type = 'twob')
plot(so$os)
gm = gramian(so$os) #verification of the orthogonality
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -1.471562e-14
#-------------------------------------------------#
#---Twosided osplines, non equally spaced knots---#
#-------------------------------------------------#
so = splinet(Bsplines=sody$bs, type = 'twob')
plot(so$os)
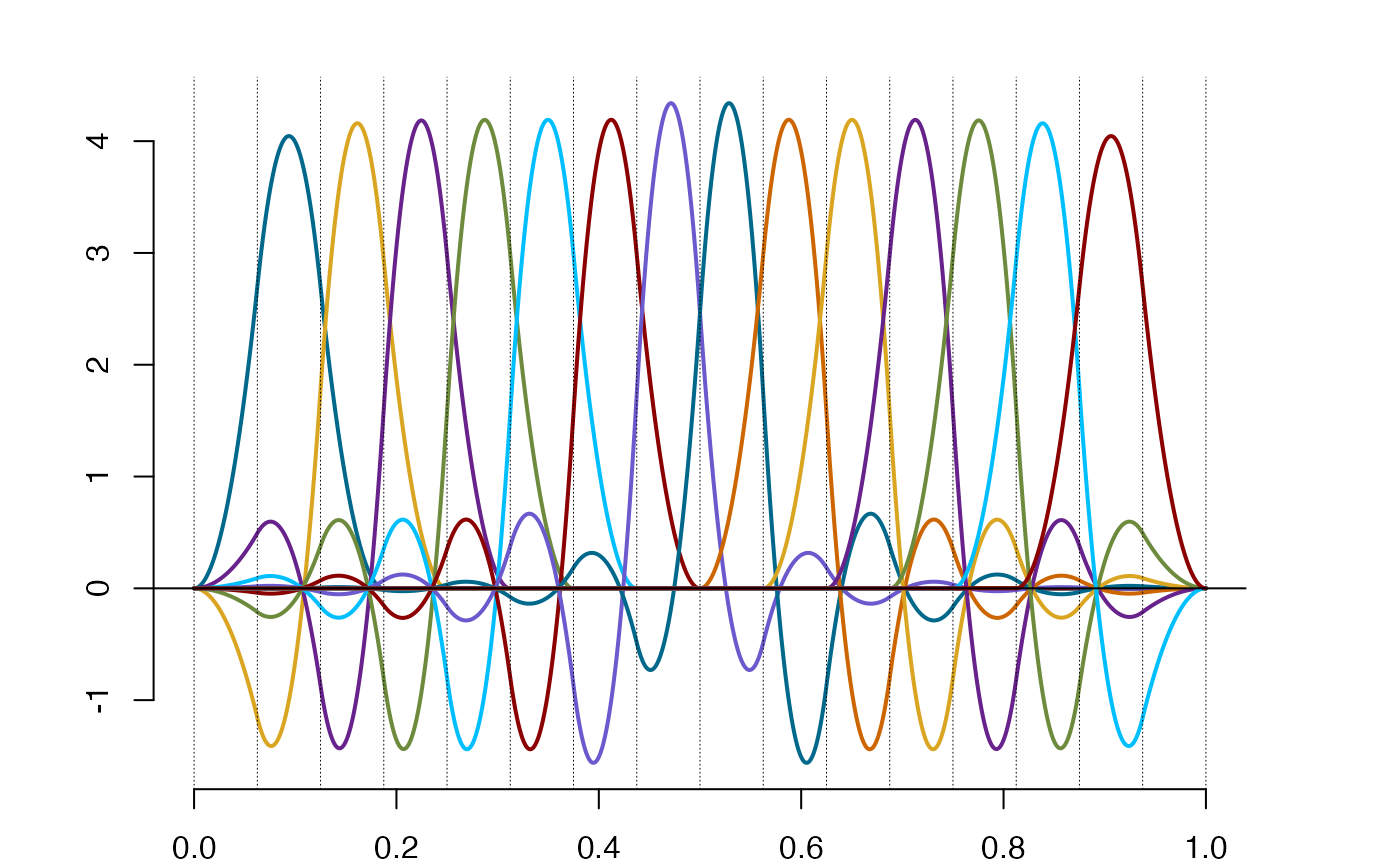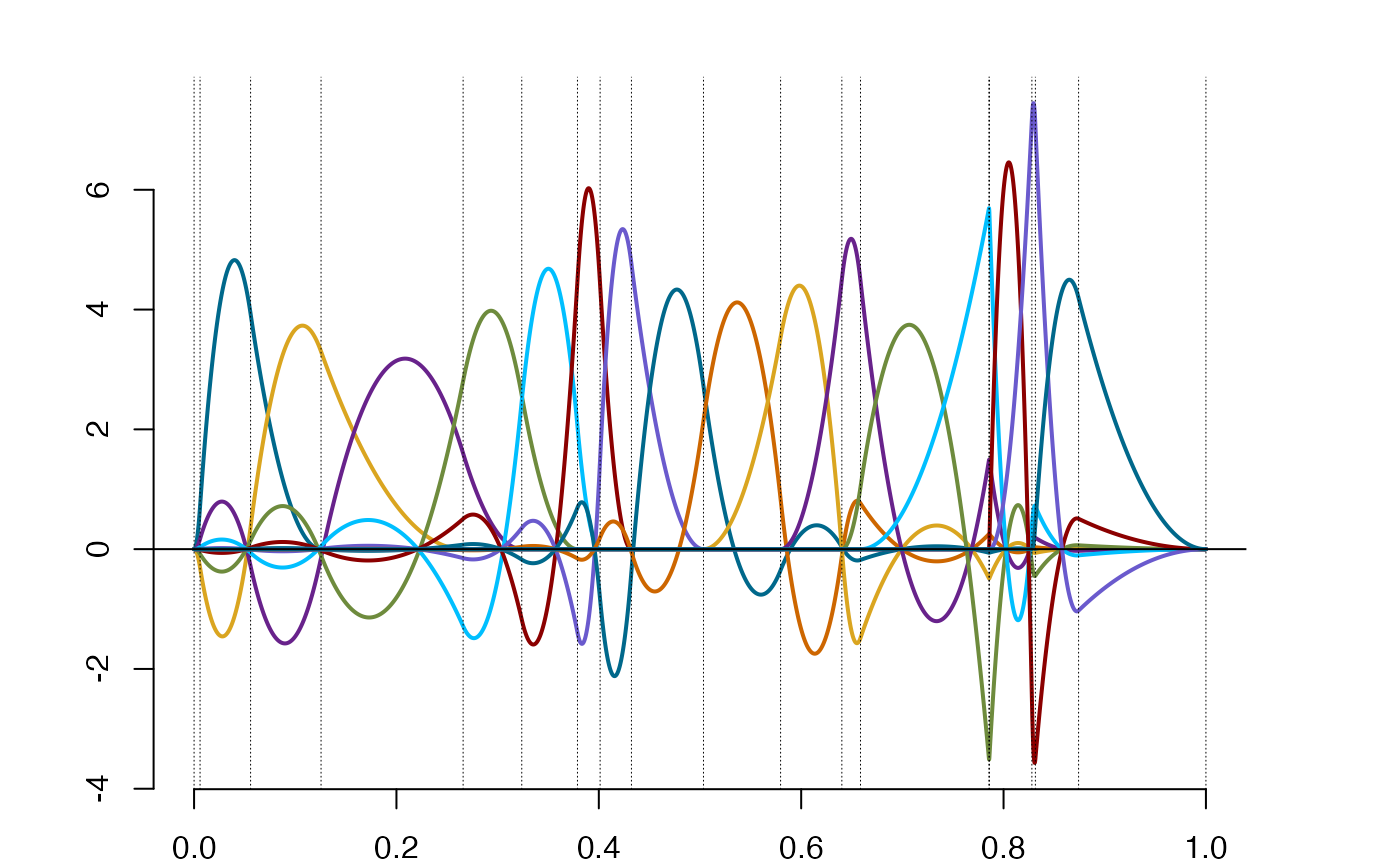gm = gramian(so$os) #verification of the orthogonality
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] 1.40572e-14
#--------------------------------------------#
#---Periodic splinet, equally spaced knots---#
#--------------------------------------------#
k=2 # order
n_knots = 12 # number of knots
xi = seq(0, 1, length.out = n_knots)
so = splinet(xi, k, periodic = TRUE)
plot(so$bs) #Plotting B-splines
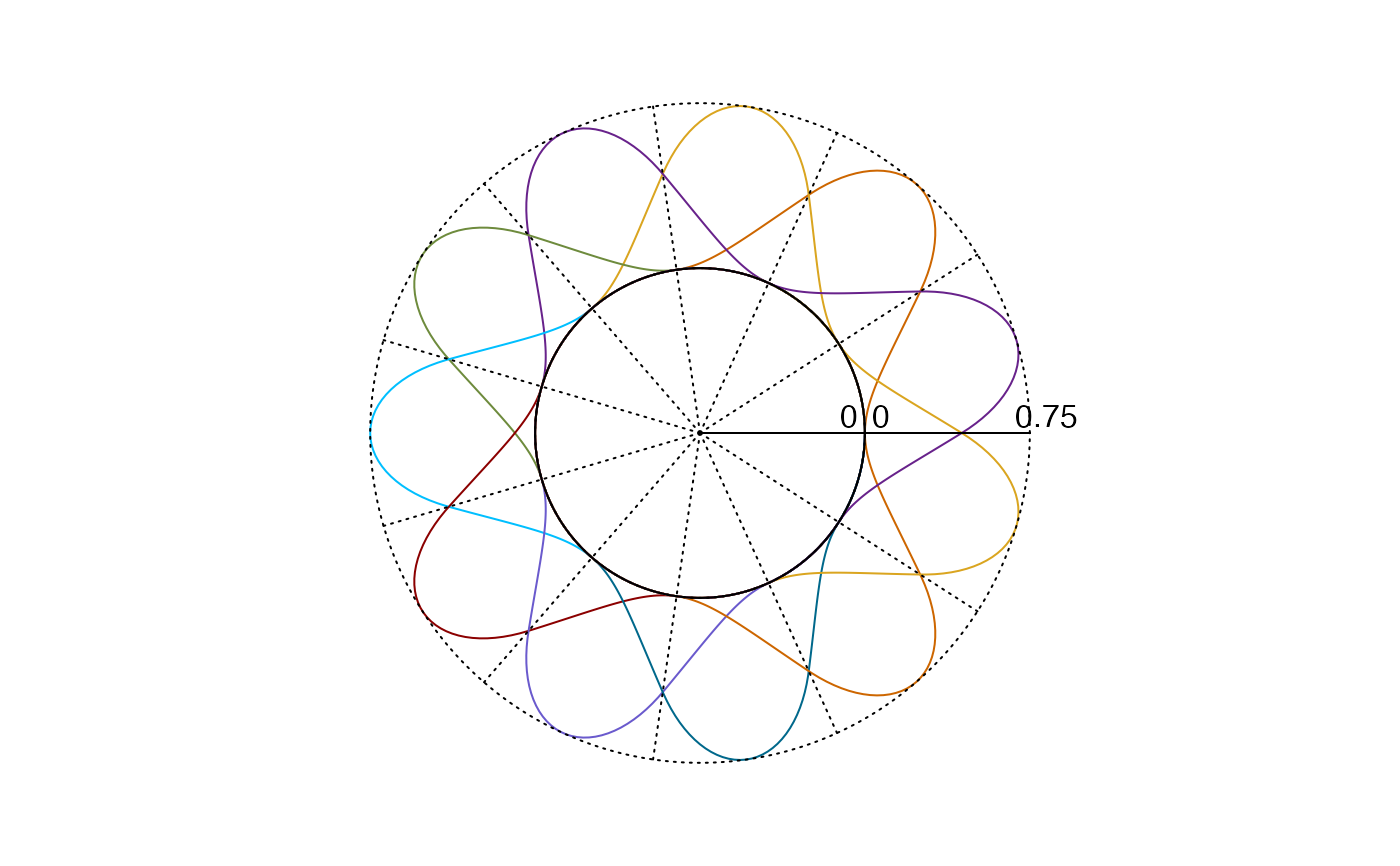plot(so$os) #Plotting Splinet
#Verifying the orthogonalization
gm = gramian(so$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -6.644666e-18
#An example of the dyadic structure with equally spaced knots
k=3
N=3
n_knots=2^N*k-1 #the number of internal knots for the dyadic case
xi = seq(0, 1, length.out = n_knots+2)
so = splinet(xi, periodic = TRUE)
plot(so$bs,type="simple") #Plotting B-splines in a single simple plot
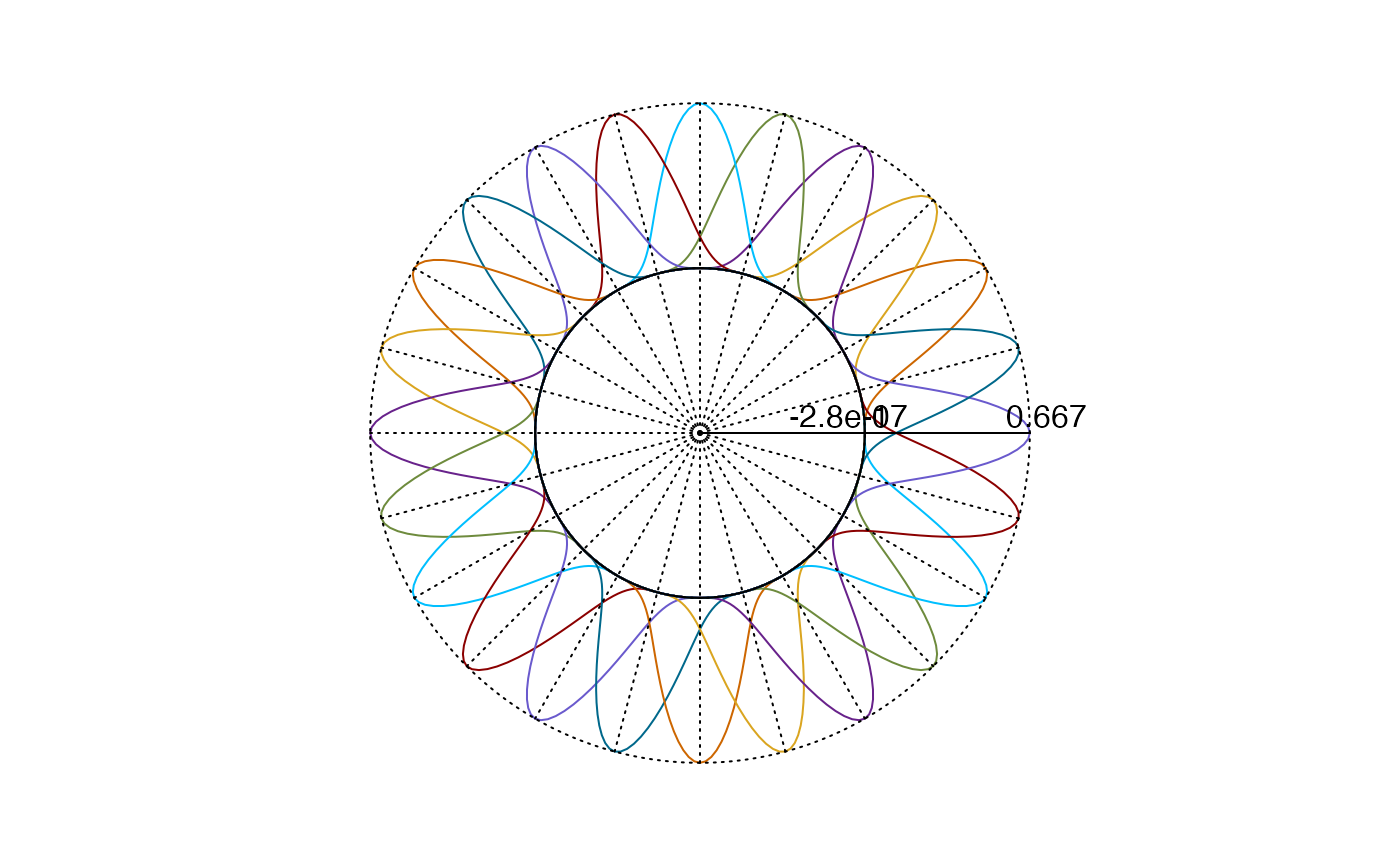plot(so$os,type="simple")
plot(so$os) #Plotting the splinet on the dyadic net of support intervals
so=splinet(xi, Bsplines=so$bs, type='gsob') #Obtaining the Gram-Schmidt orthogonalization
plot(so$os,type="simple") #Without computing B-splines again
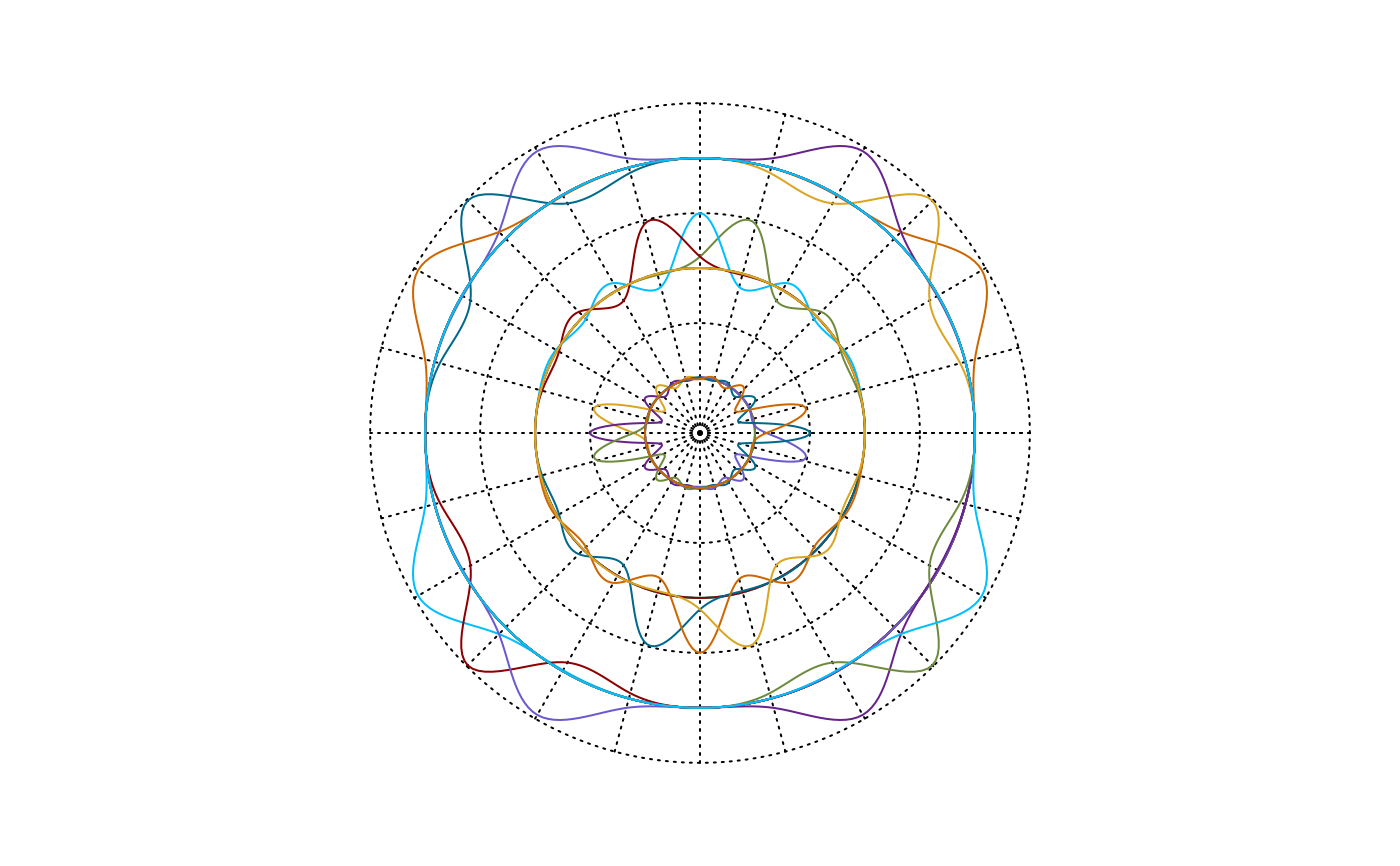so=splinet(xi, Bsplines=so$bs , type='twob') #Obtaining the symmetrize orthogonalization
plot(so$os,type="simple")
#-------------------------------------#
#---Splinet, unequally spaced knots---#
#-------------------------------------#
n_knots=25
xi = c(0, sort(runif(n_knots)), 1)
sone = splinet(xi, k, periodic = TRUE)
plot(sone$bs, type='dyadic') #Plotting B-splines
plot(sone$os) #Plotting Splinet
#Verifying the orthogonalization
gm = gramian(sone$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] 3.920568e-13
#------------------------------------------#
#---Dyadic splinet, equally spaced knots---#
#------------------------------------------#
k = 2 # order
N = 3 # support level
n_so = k*(2^N-1) # number of splines in a dyadic structure with N and k
n_knots = n_so + k + 1 # number of knots
xi = seq(0, 1, length.out = n_knots)
sodyeq = splinet(xi, k, periodic = TRUE)
plot(sodyeq$bs) #Plotting B-splines
plot(sodyeq$os) #Plotting Splinet
#Verifying the orthogonalization
gm = gramian(sodyeq$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -1.479494e-14
#--------------------------------------------#
#---Dyadic splinet, unequally spaced knots---#
#--------------------------------------------#
xi = c(0, sort(runif(n_knots)), 1)
sody = splinet(xi, k, periodic = TRUE)
plot(sody$bs) #Plotting B-splines
plot(sody$os) #Plotting Splinet
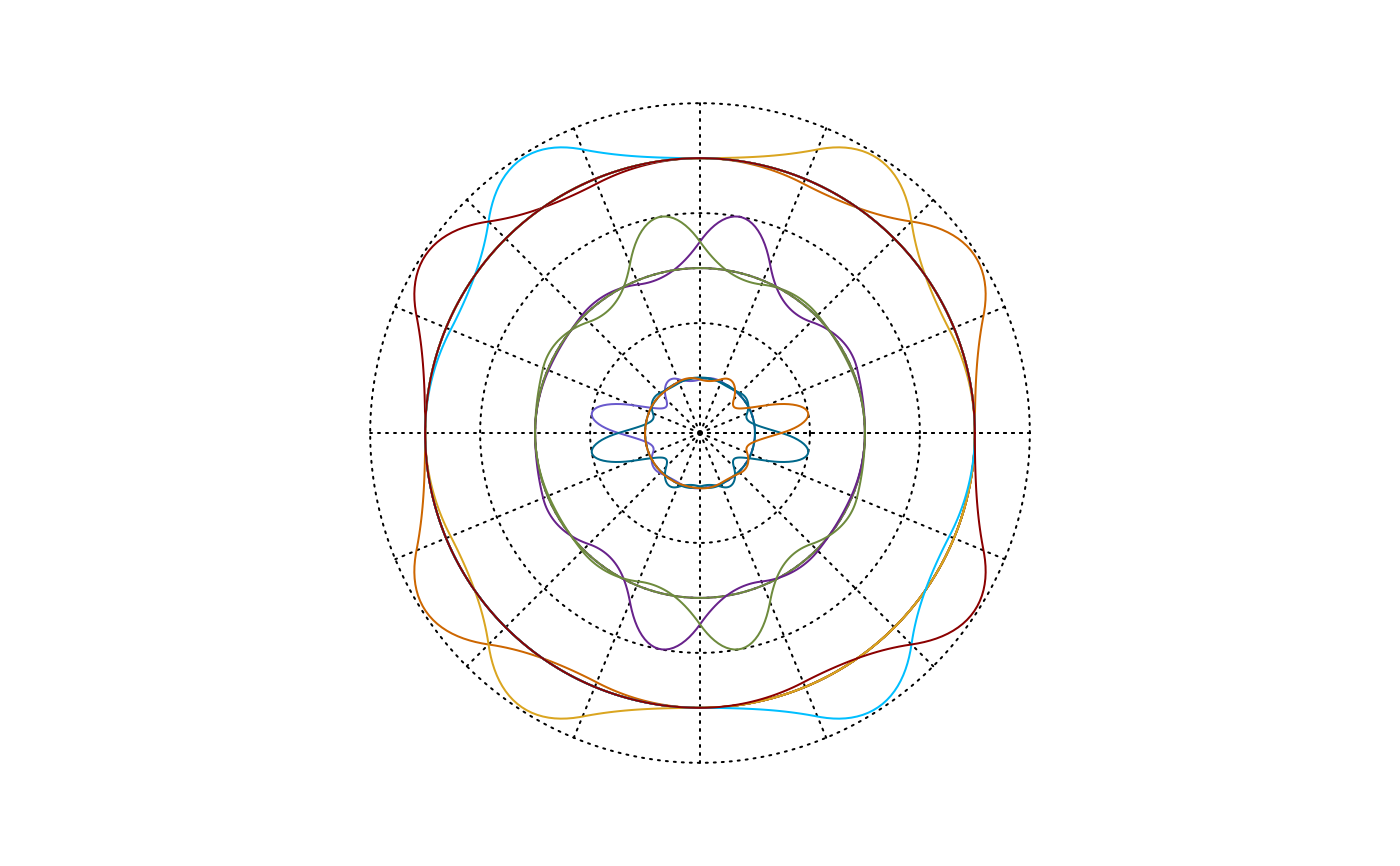#Verifying the orthogonalization
gm = gramian(sody$os) #evaluation of the inner products
diag(gm)
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
sum(gm - diag(diag(gm)))
#> [1] -1.505296e-14