Derivatives of splines

The function generates a Splinets-object which contains the first order derivatives of all the splines from the input Splinets-object. The function also verifies the support set of the output to provide the accurate information about the support sets by excluding regions over which the original function is constant.

Usage

deriva(object, epsilon = 1e-07)

Arguments

object: Splinets object of the smoothness order k;
epsilon: positive number, controls removal of knots from the support; If the derivative is smaller than this number, it is considered to be zero and the corresponding knots are removed from the support.The default value is 1e-7.

Value

A Splinets-object of the order k-1 that also contains the updated information about the support set.

References

Liu, X., Nassar, H., Podg\(\mbox{\'o}\)rski, K. "Dyadic diagonalization of positive definite band matrices and efficient B-spline orthogonalization." Journal of Computational and Applied Mathematics (2022) <https://doi.org/10.1016/j.cam.2022.114444>.

Podg\(\mbox{\'o}\)rski, K. (2021) "Splinets – splines through the Taylor expansion, their support sets and orthogonal bases." <arXiv:2102.00733>.

Nassar, H., Podg\(\mbox{\'o}\)rski, K. (2023) "Splinets 1.5.0 – Periodic Splinets." <arXiv:2302.07552>

Examples

#-------------------------------------------------------#
#--- Generating the deriviative functions of splines ---#
#-------------------------------------------------------#
n=13; k=4
set.seed(5)
xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
spl=construct(xi,k,matrix(rnorm((n+2)*(k+1)),ncol=(k+1))) #constructing three splines
#> 
#> Using  method RRM to correct the derivative matrix entries.
#> 
#> 
#> DIAGNOSTIC CHECK of a SPLINETS object
#> 
#> THE KNOTS:  
#> 
#> 
#> THE SUPPORT SETS:  
#> 
#> The support sets for the splines are equal to the entire range of knots.
#> 
#> 
#> THE DERIVATIVES AT THE KNOTS:  
#> 
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> 
#>  The spline 1 'ths highest derivative at the central knot is zero.
#> Now it is set to zero.
#> 
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.421221 .
#> 
#> 
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#> 
#> 
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#> 
#> 
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#> 
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl, construct(xi,k,matrix(rnorm((n+2)*(k+1)),ncol=(k+1)))) 
#> 
#> Using  method RRM to correct the derivative matrix entries.
#> 
#> 
#> DIAGNOSTIC CHECK of a SPLINETS object
#> 
#> THE KNOTS:  
#> 
#> 
#> THE SUPPORT SETS:  
#> 
#> The support sets for the splines are equal to the entire range of knots.
#> 
#> 
#> THE DERIVATIVES AT THE KNOTS:  
#> 
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> 
#>  The spline 1 'ths highest derivative at the central knot is zero.
#> Now it is set to zero.
#> 
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.555902 .
#> 
#> 
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#> 
#> 
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#> 
#> 
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#> 
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl, construct(xi,k,matrix(rnorm((n+2)*(k+1)),ncol=(k+1)))) 
#> 
#> Using  method RRM to correct the derivative matrix entries.
#> 
#> 
#> DIAGNOSTIC CHECK of a SPLINETS object
#> 
#> THE KNOTS:  
#> 
#> 
#> THE SUPPORT SETS:  
#> 
#> The support sets for the splines are equal to the entire range of knots.
#> 
#> 
#> THE DERIVATIVES AT THE KNOTS:  
#> 
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> 
#>  The spline 1 'ths highest derivative at the central knot is zero.
#> Now it is set to zero.
#> 
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.35308 .
#> 
#> 
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#> 
#> 
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 3 entries of the 6 nd row counting from the end in the input will be changed in the output.
#> 
#> 
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#> 
#> The matrix derivative is now corrected by method RRM .
# calculate the derivative of splines
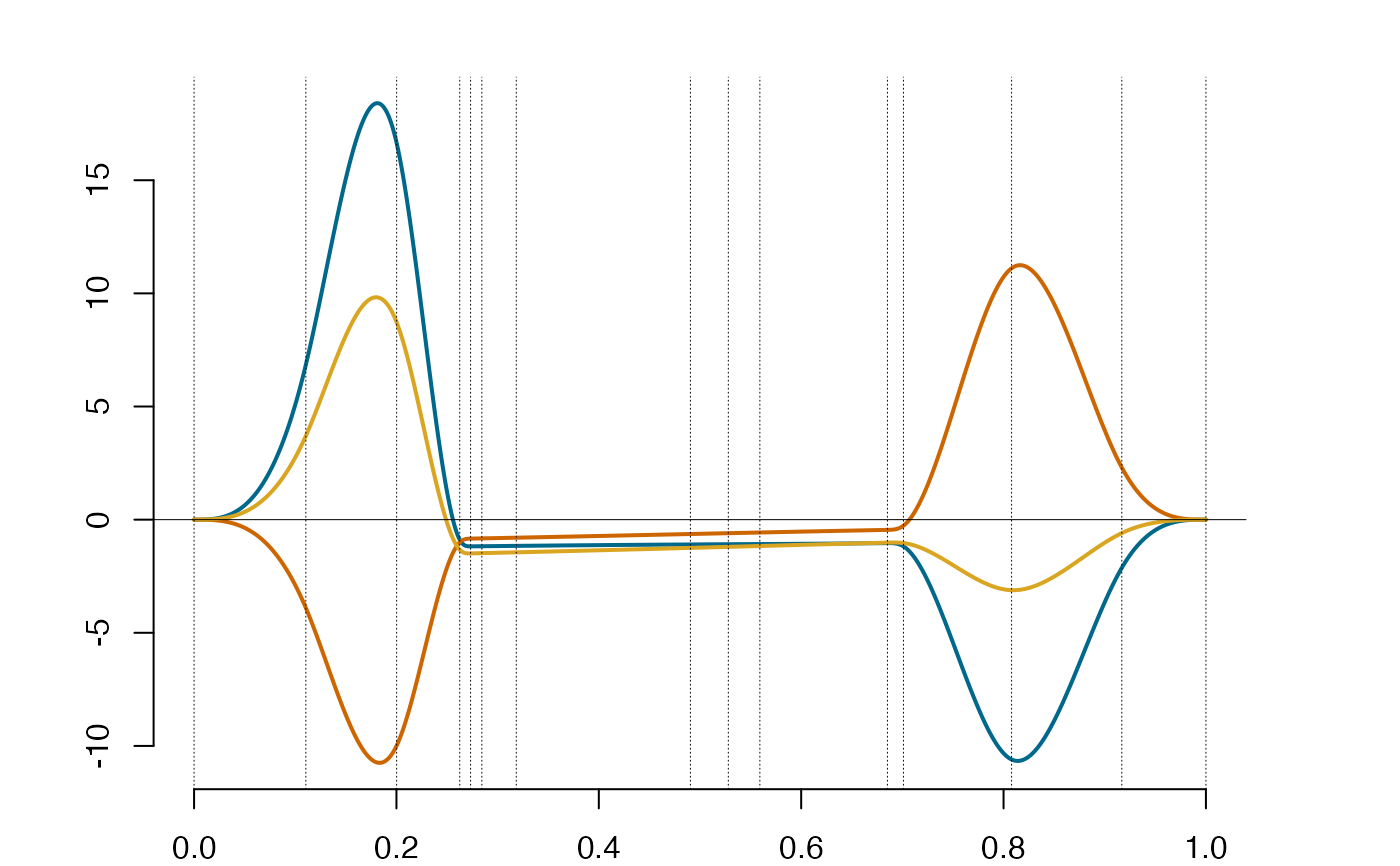
dspl = deriva(spl)
plot(spl)

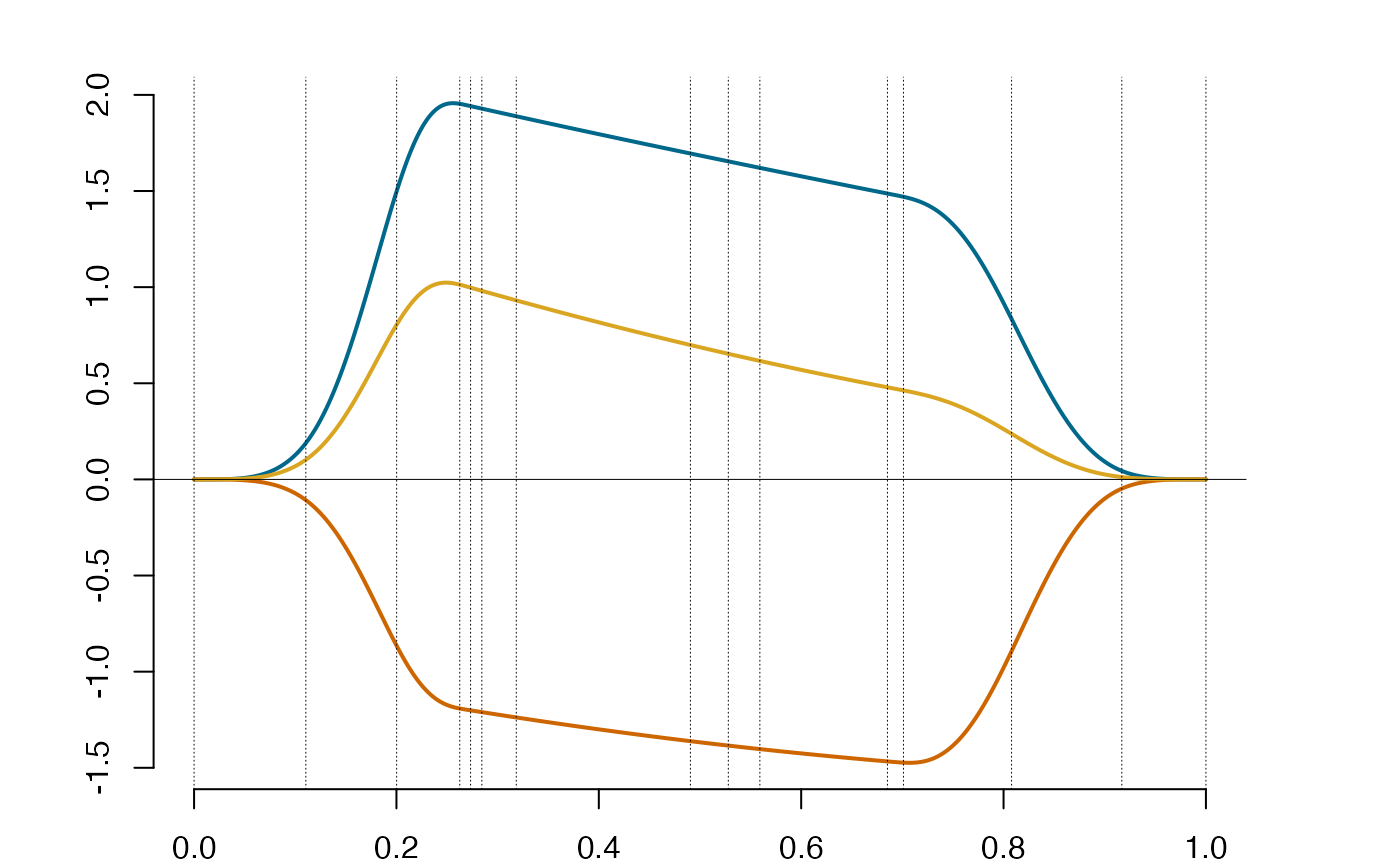plot(dspl)


#----------------------------------------------#
#--- Examples with different support ranges ---#
#----------------------------------------------#

n=25; k=3
xi=seq(0,1,by=1/(n+1));
set.seed(5)
#Defining support ranges for three splines
supp=matrix(c(2,12,4,20,6,25),byrow=TRUE,ncol=2)
#Initial random matrices of the derivative for each spline
SS1=matrix(rnorm((supp[1,2]-supp[1,1]+1)*(k+1)),ncol=(k+1)) 
SS2=matrix(rnorm((supp[2,2]-supp[2,1]+1)*(k+1)),ncol=(k+1)) 
SS3=matrix(rnorm((supp[3,2]-supp[3,1]+1)*(k+1)),ncol=(k+1)) 
spl=construct(xi,k,SS1,supp[1,]) #constructing the first correct spline
#> 
#> Using  method RRM to correct the derivative matrix entries.
#> 
#> 
#> DIAGNOSTIC CHECK of a SPLINETS object
#> 
#> THE KNOTS:  
#> 
#> 
#> THE SUPPORT SETS:  
#> 
#> 
#> 
#> THE DERIVATIVES AT THE KNOTS:  
#> 
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> 
#> Spline 1 support 1 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 1 's highest derivative value at the central knot has been made equal to zero.
#> 
#> The matrix of derivatives at the knots for spline 1 , support 1  does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.31684 .
#> 
#> 
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1  support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
nspl=construct(xi,k,SS2,supp[2,])
#> 
#> Using  method RRM to correct the derivative matrix entries.
#> 
#> 
#> DIAGNOSTIC CHECK of a SPLINETS object
#> 
#> THE KNOTS:  
#> 
#> 
#> THE SUPPORT SETS:  
#> 
#> 
#> 
#> THE DERIVATIVES AT THE KNOTS:  
#> 
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> 
#> Spline 1 support 1 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 1 's highest derivative value at the central knot has been made equal to zero.
#> 
#> The matrix of derivatives at the knots for spline 1 , support 1  does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.294431 .
#> 
#> 
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1  support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl,nspl) #the second and the first ones
nspl=construct(xi,k,SS3,supp[3,])
#> 
#> Using  method RRM to correct the derivative matrix entries.
#> 
#> 
#> DIAGNOSTIC CHECK of a SPLINETS object
#> 
#> THE KNOTS:  
#> 
#> 
#> THE SUPPORT SETS:  
#> 
#> 
#> 
#> THE DERIVATIVES AT THE KNOTS:  
#> 
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> 
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1  highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#> 
#> The matrix of derivatives at the knots for spline 1 , support 1  does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.640386 .
#> 
#> 
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1  support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl,nspl) #the third is added

der_spl = deriva(spl)
par(mar=c(1,1,1,1))
par(mfrow=c(2,1))
plot(der_spl)
plot(spl)

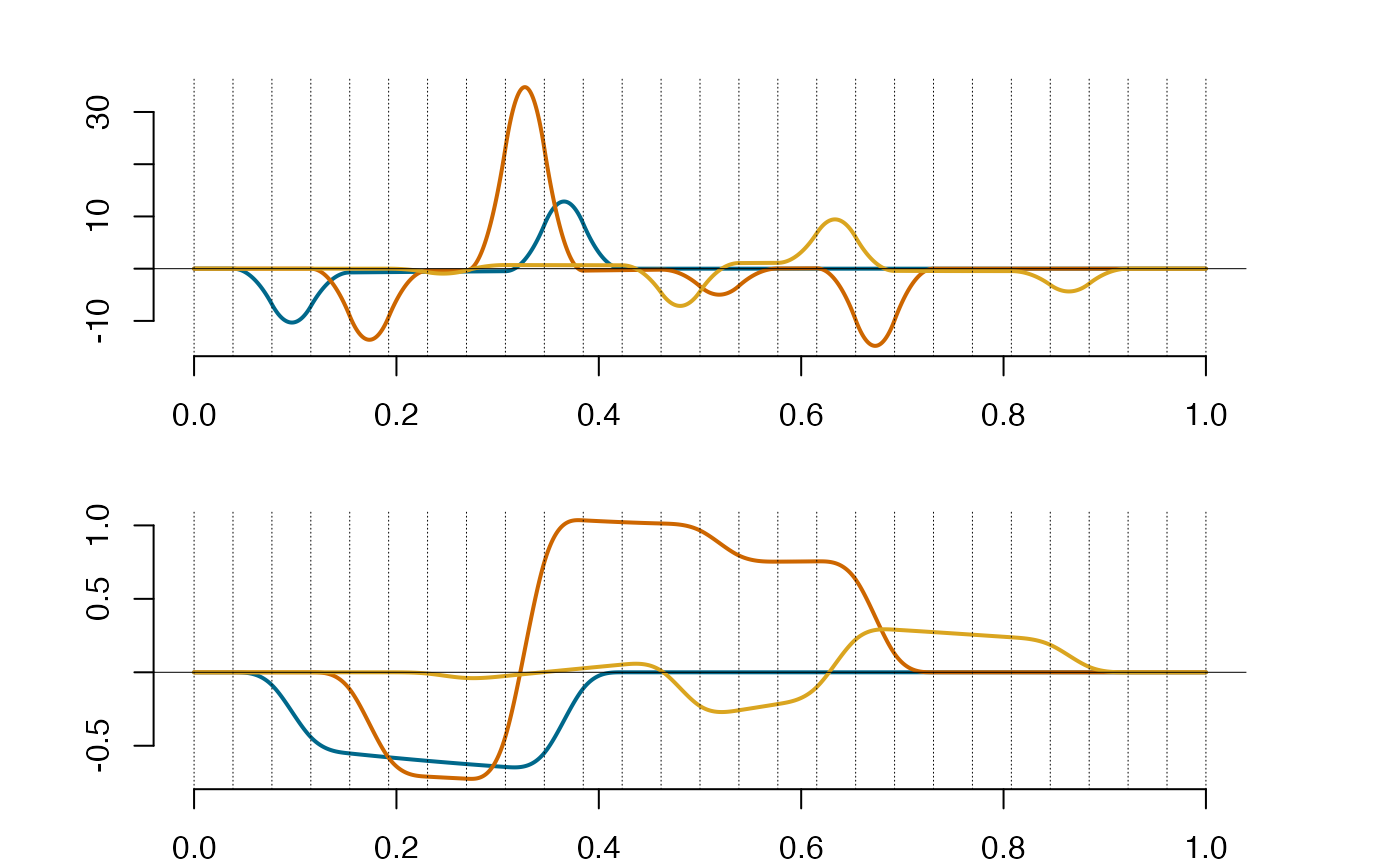par(mfrow=c(1,1))

Usage

Arguments

Value

References

See also

Examples