The function generates the indefinite integrals for given input splines. The integral is a function of the upper limit of the definite integral and is a spline of the higher order that does not satisfy the zero boundary conditions at the RHS endpoint, unless the definite integral over the whole range is equal to zero. Moreover, the support of the function is extended in the RHS up to the RHS end point unless the definite integral of the input is zero, in which the case the support is extracted from the obtained spline.
Details
The value on the RHS is not zero, so the zero boundary condition typically is not satisfied and the support is is extended to the RHS end of the whole domain of splines. However, the function returns proper support if the original spline is a derivative of a spline that satisfies the boundary conditons.
References
Liu, X., Nassar, H., Podg\(\mbox{\'o}\)rski, K. "Dyadic diagonalization of positive definite band matrices and efficient B-spline orthogonalization." Journal of Computational and Applied Mathematics (2022) <https://doi.org/10.1016/j.cam.2022.114444>.
Podg\(\mbox{\'o}\)rski, K. (2021)
"Splinets – splines through the Taylor expansion, their support sets and orthogonal bases." <arXiv:2102.00733>.
Nassar, H., Podg\(\mbox{\'o}\)rski, K. (2023) "Splinets 1.5.0 – Periodic Splinets." <arXiv:2302.07552>
Examples
#------------------------------------#
#--- Generate indefinite integral ---#
#------------------------------------#
n=18; k=3; xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
# generate a random matrix S
set.seed(5)
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1))
spl=construct(xi,k,S) #constructing a spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> Spline 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> The spline 1 'ths highest derivative at the two central knots has been made equal by averaging SLOT 'der'.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.292652 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 5 knots, the first 2 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 5 knots, the first 2 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The matrix derivative is now corrected by method RRM .
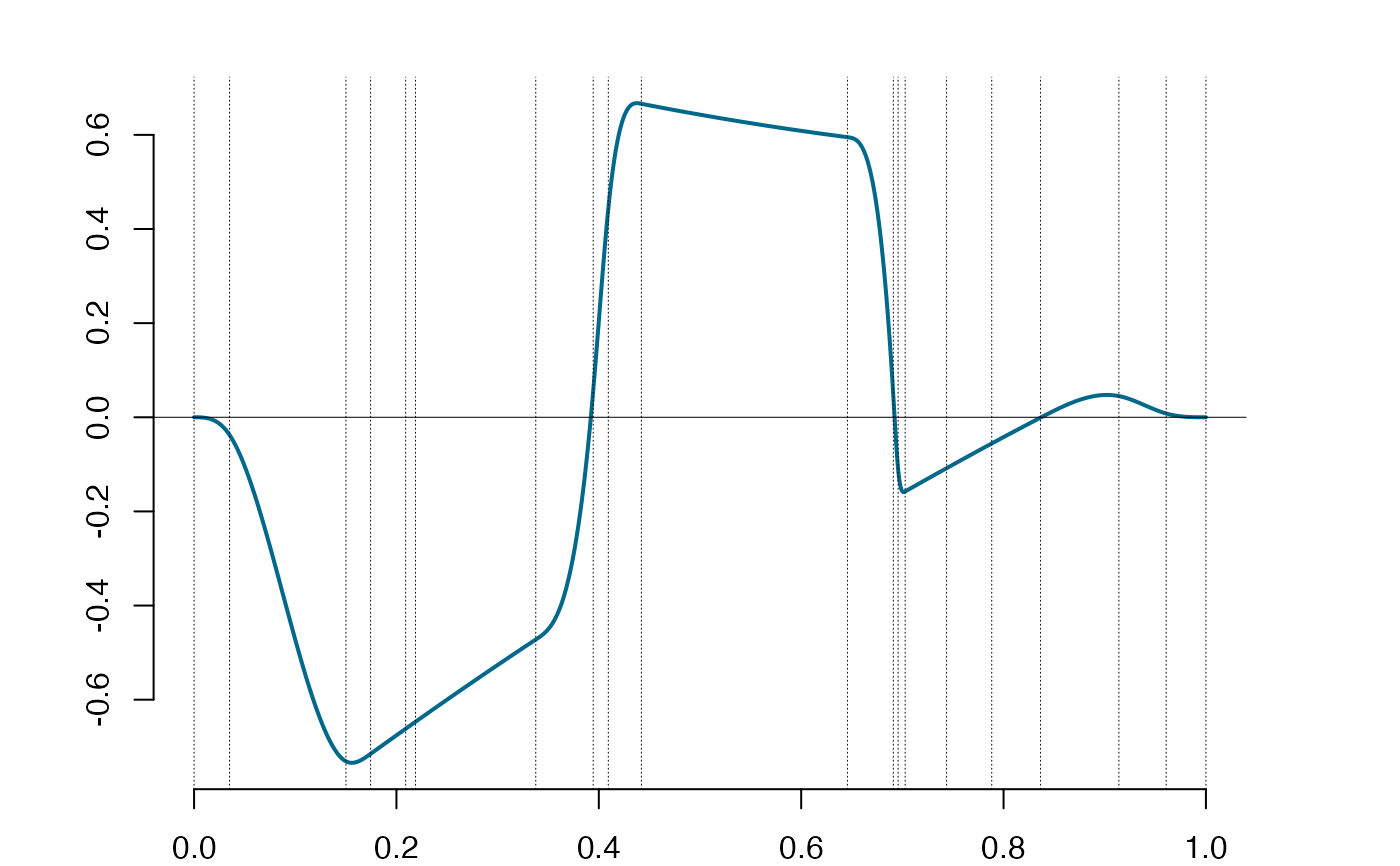
plot(spl)
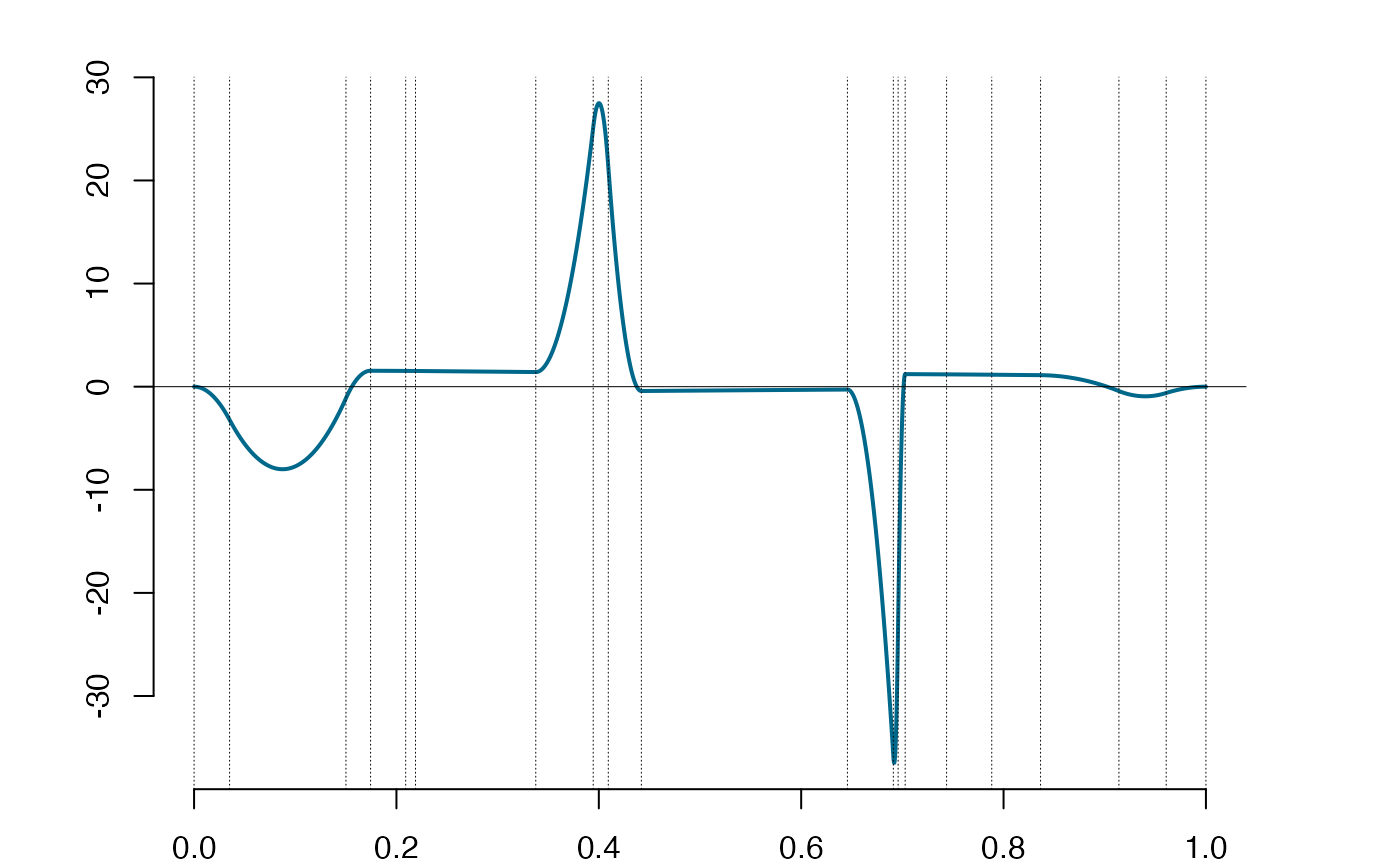
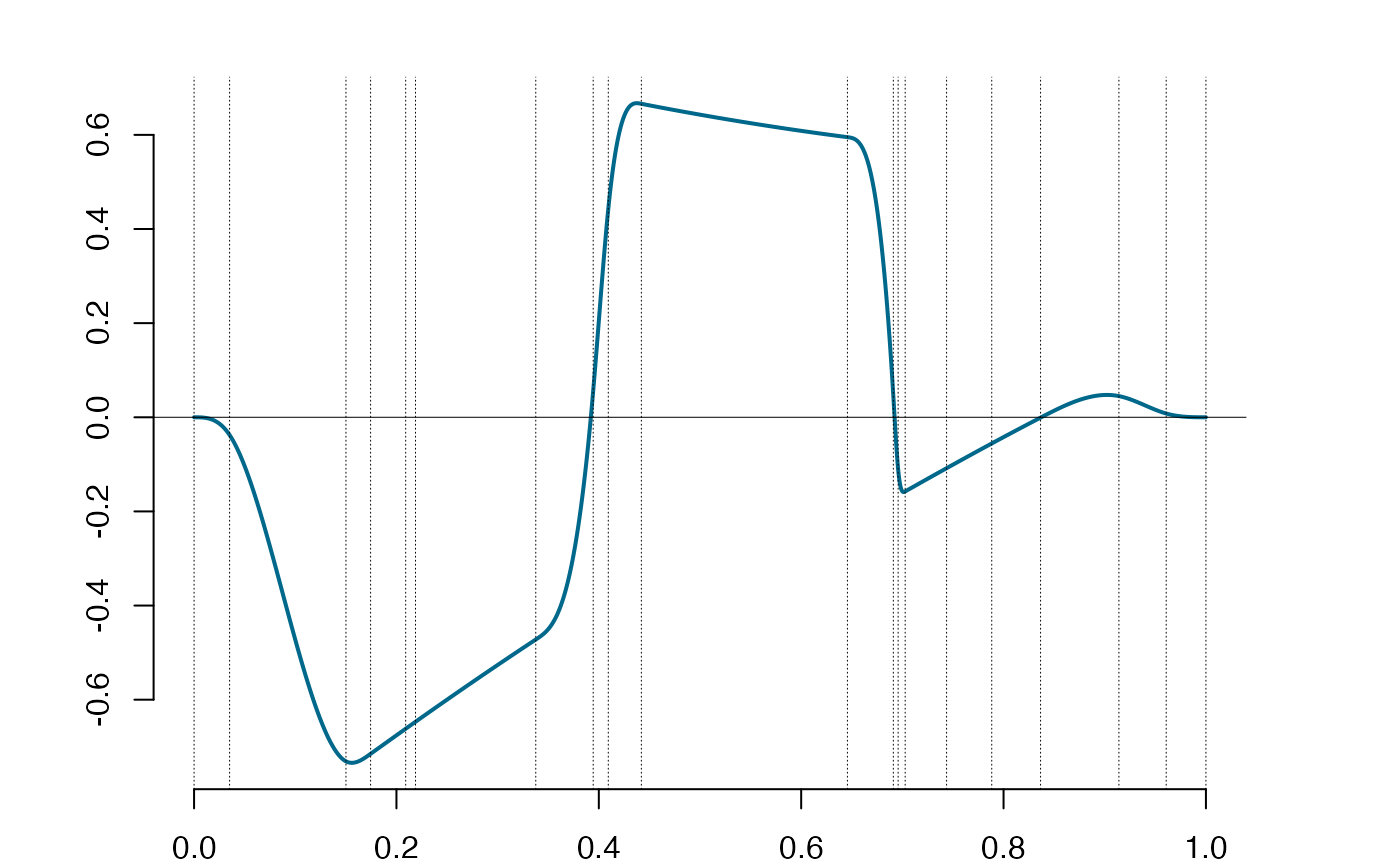 dspl = deriva(spl) #derivative
plot(dspl)
dspl = deriva(spl) #derivative
plot(dspl)
 is.splinets(dspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 20 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 2
#> Support: Not the full range support, a single support interval for each spline.
#> $Er
#> [1] 1.059186e-20
#>
dintegra(dspl) #the definite integral is 0 (the boundary conditions for 'spl')
#> Spline ID dIntegral
#> [1,] 1 1.250736e-15
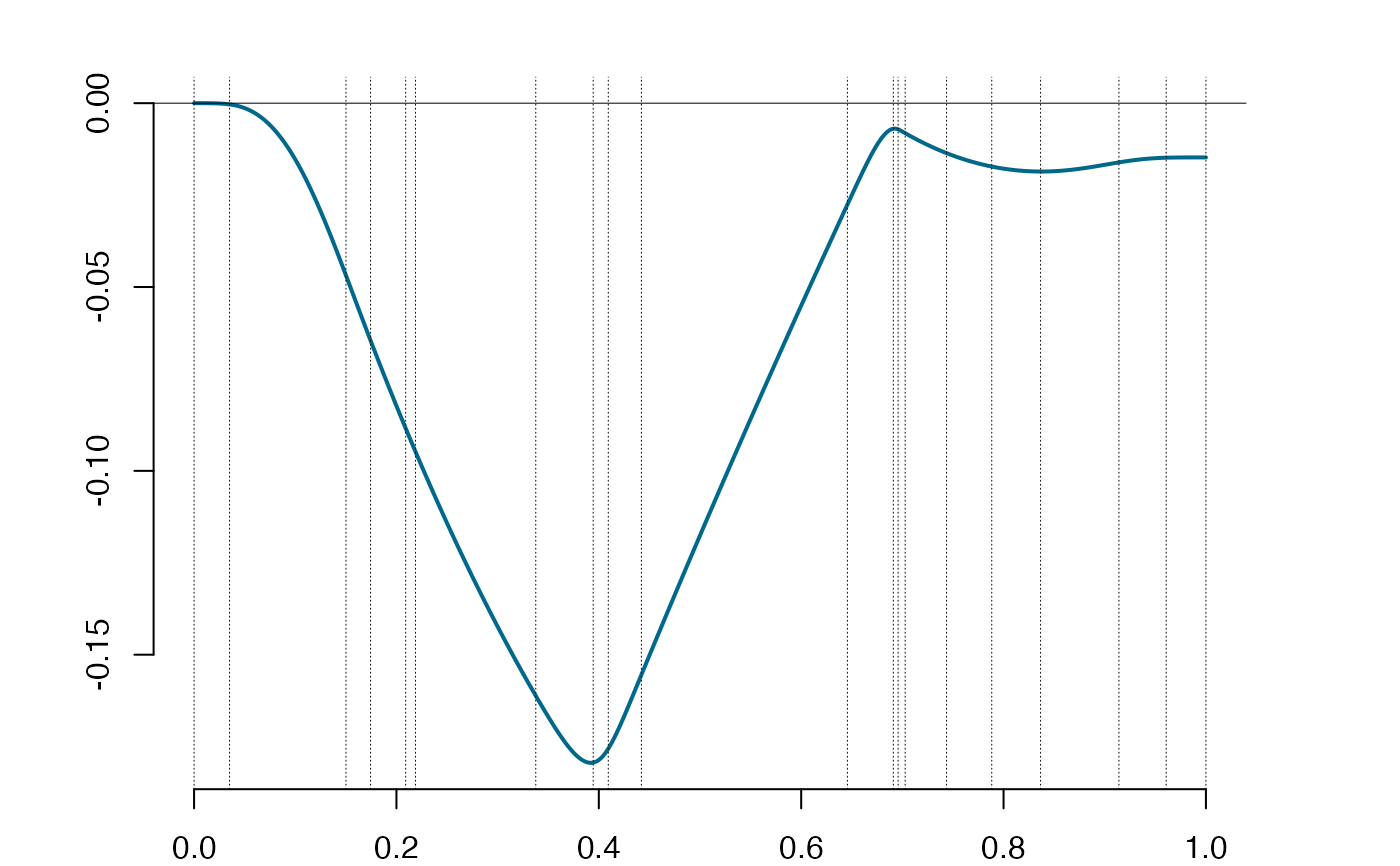
ispl = integra(spl) #the integral of a spline
plot(ispl) #the boundary condition on the rhs not satisfied (non-zero value)
is.splinets(dspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 20 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 2
#> Support: Not the full range support, a single support interval for each spline.
#> $Er
#> [1] 1.059186e-20
#>
dintegra(dspl) #the definite integral is 0 (the boundary conditions for 'spl')
#> Spline ID dIntegral
#> [1,] 1 1.250736e-15
ispl = integra(spl) #the integral of a spline
plot(ispl) #the boundary condition on the rhs not satisfied (non-zero value)
 ispl@smorder
#> [1] 4
is.splinets(ispl) #the object does not satisfy the boundary condition for the spline
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.001738661 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#> $is
#> [1] FALSE
#>
#> $robject
#> splines
#> Knots: 20 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 0.0002176519
#>
spll = integra(dspl)
plot(spll)
ispl@smorder
#> [1] 4
is.splinets(ispl) #the object does not satisfy the boundary condition for the spline
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.001738661 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#> $is
#> [1] FALSE
#>
#> $robject
#> splines
#> Knots: 20 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 0.0002176519
#>
spll = integra(dspl)
plot(spll)
 is.splinets(spll) #the boundary conditions of the integral of the derivative satisfied.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 20 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 3
#> Support: The full support range for each spline.
#> $Er
#> [1] 1.059186e-20
#>
#----------------------------------------------#
#--- Examples with different support ranges ---#
#----------------------------------------------#
n=25; k=2;
set.seed(5)
xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
#Defining support ranges for three splines
supp=matrix(c(2,12,4,20,6,25),byrow=TRUE,ncol=2)
#Initial random matrices of the derivative for each spline
SS1=matrix(rnorm((supp[1,2]-supp[1,1]+1)*(k+1)),ncol=(k+1))
SS2=matrix(rnorm((supp[2,2]-supp[2,1]+1)*(k+1)),ncol=(k+1))
SS3=matrix(rnorm((supp[3,2]-supp[3,1]+1)*(k+1)),ncol=(k+1))
spl=construct(xi,k,SS1,supp[1,]) #constructing the first proper spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.576956 .
#>
#>
#> Correction of the LHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
nspl=construct(xi,k,SS2,supp[2,],'CRFC')
#>
#> Using method CRFC to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.33174 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.The zero boundary conditions are not satisfied.
#> The correction of the first and last rows of the derivative matrix has been made.
#>
#>
#> The highest order derivative at the central knot is not equal to zero.
#> It has been made equal to zero now.
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The matrix derivative is now corrected by method CRFC .
spl=gather(spl,nspl) #the second and the first together
nspl=construct(xi,k,SS3,supp[3,],'CRLC')
#>
#> Using method CRLC to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 - highest derivative is not symmetric at the center (equal values at the two central knots).
#> The two values have been made equal by averaging.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.41863 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.The zero boundary conditions are not satisfied.
#> The correction of the first and last rows of the derivative matrix has been made.
#>
#>
#> The highest order derivative is not symmetrically defined at the center.
#> The values at the two central knots should be equal.
#> The highest order derivative values at the two central knots
#> have been made equal by averaging the two central values.
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The matrix derivative is now corrected by method CRLC .
spl=gather(spl,nspl) #the third is added
plot(spl)
is.splinets(spll) #the boundary conditions of the integral of the derivative satisfied.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 20 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 3
#> Support: The full support range for each spline.
#> $Er
#> [1] 1.059186e-20
#>
#----------------------------------------------#
#--- Examples with different support ranges ---#
#----------------------------------------------#
n=25; k=2;
set.seed(5)
xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
#Defining support ranges for three splines
supp=matrix(c(2,12,4,20,6,25),byrow=TRUE,ncol=2)
#Initial random matrices of the derivative for each spline
SS1=matrix(rnorm((supp[1,2]-supp[1,1]+1)*(k+1)),ncol=(k+1))
SS2=matrix(rnorm((supp[2,2]-supp[2,1]+1)*(k+1)),ncol=(k+1))
SS3=matrix(rnorm((supp[3,2]-supp[3,1]+1)*(k+1)),ncol=(k+1))
spl=construct(xi,k,SS1,supp[1,]) #constructing the first proper spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.576956 .
#>
#>
#> Correction of the LHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
nspl=construct(xi,k,SS2,supp[2,],'CRFC')
#>
#> Using method CRFC to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.33174 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 4 knots, the first 1 entries of the 4 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.The zero boundary conditions are not satisfied.
#> The correction of the first and last rows of the derivative matrix has been made.
#>
#>
#> The highest order derivative at the central knot is not equal to zero.
#> It has been made equal to zero now.
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The matrix derivative is now corrected by method CRFC .
spl=gather(spl,nspl) #the second and the first together
nspl=construct(xi,k,SS3,supp[3,],'CRLC')
#>
#> Using method CRLC to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 - highest derivative is not symmetric at the center (equal values at the two central knots).
#> The two values have been made equal by averaging.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.41863 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.The zero boundary conditions are not satisfied.
#> The correction of the first and last rows of the derivative matrix has been made.
#>
#>
#> The highest order derivative is not symmetrically defined at the center.
#> The values at the two central knots should be equal.
#> The highest order derivative values at the two central knots
#> have been made equal by averaging the two central values.
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The matrix derivative is now corrected by method CRLC .
spl=gather(spl,nspl) #the third is added
plot(spl)
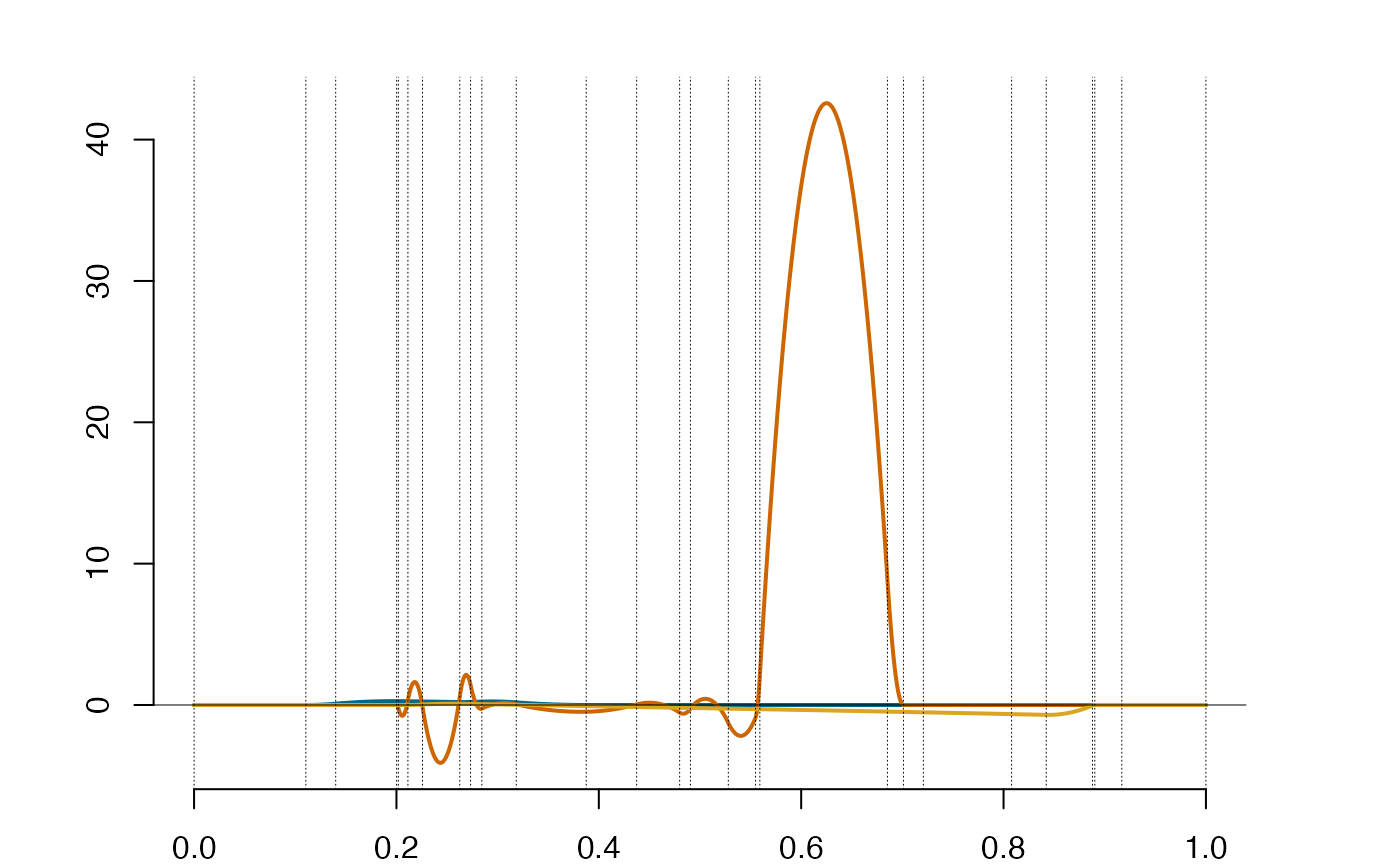 spl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
dspl = deriva(spl) #derivative of the splines
plot(dspl)
spl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
dspl = deriva(spl) #derivative of the splines
plot(dspl)
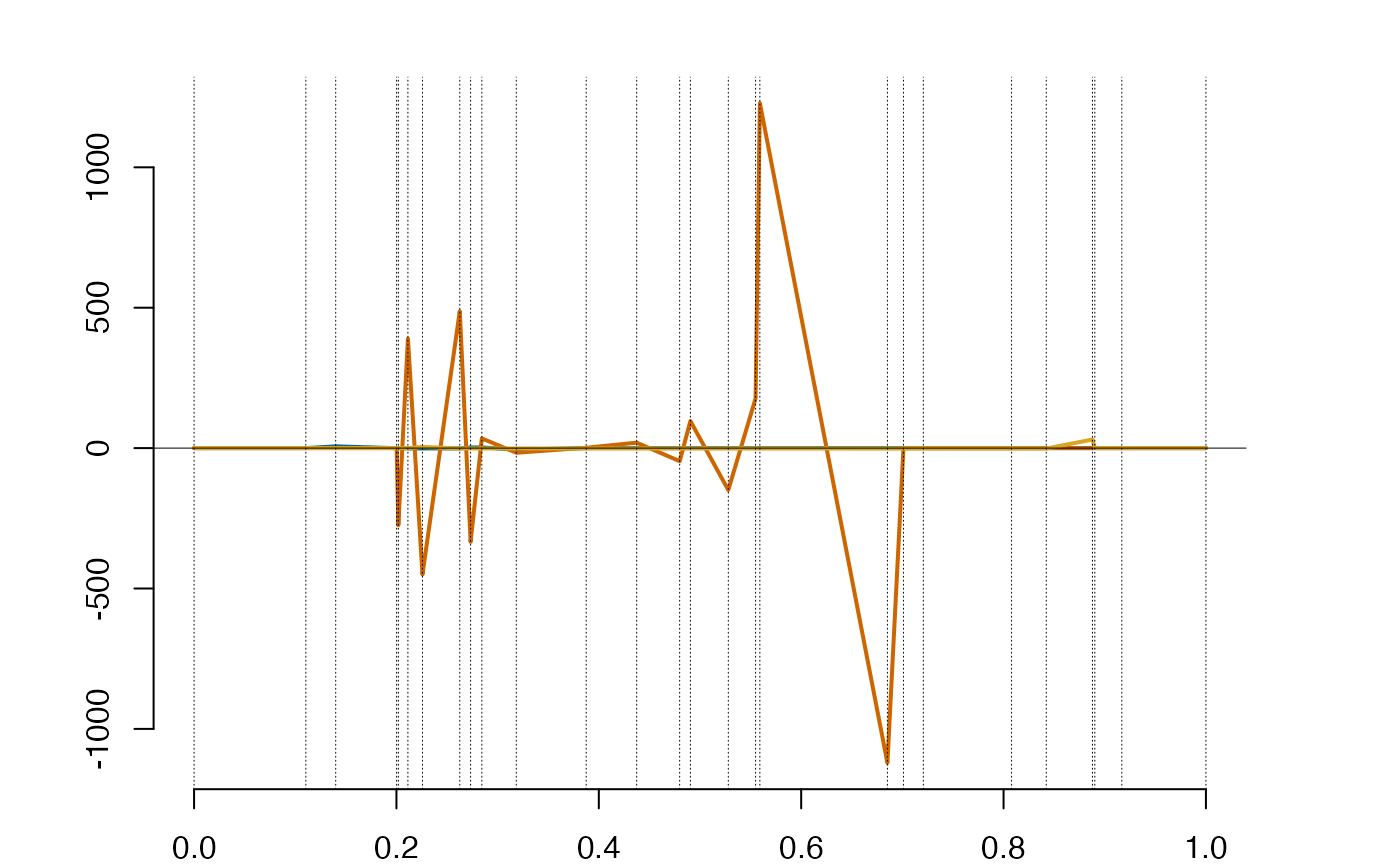 dintegra(dspl) #the definite integral over the entire range of knots is zero
#> Spline ID dIntegral
#> [1,] 1 -1.665335e-16
#> [2,] 2 -8.881784e-15
#> [3,] 3 -1.318390e-16
idspl = integra(dspl) #integral of the derivative returns the original splines
plot(idspl)
dintegra(dspl) #the definite integral over the entire range of knots is zero
#> Spline ID dIntegral
#> [1,] 1 -1.665335e-16
#> [2,] 2 -8.881784e-15
#> [3,] 3 -1.318390e-16
idspl = integra(dspl) #integral of the derivative returns the original splines
plot(idspl)
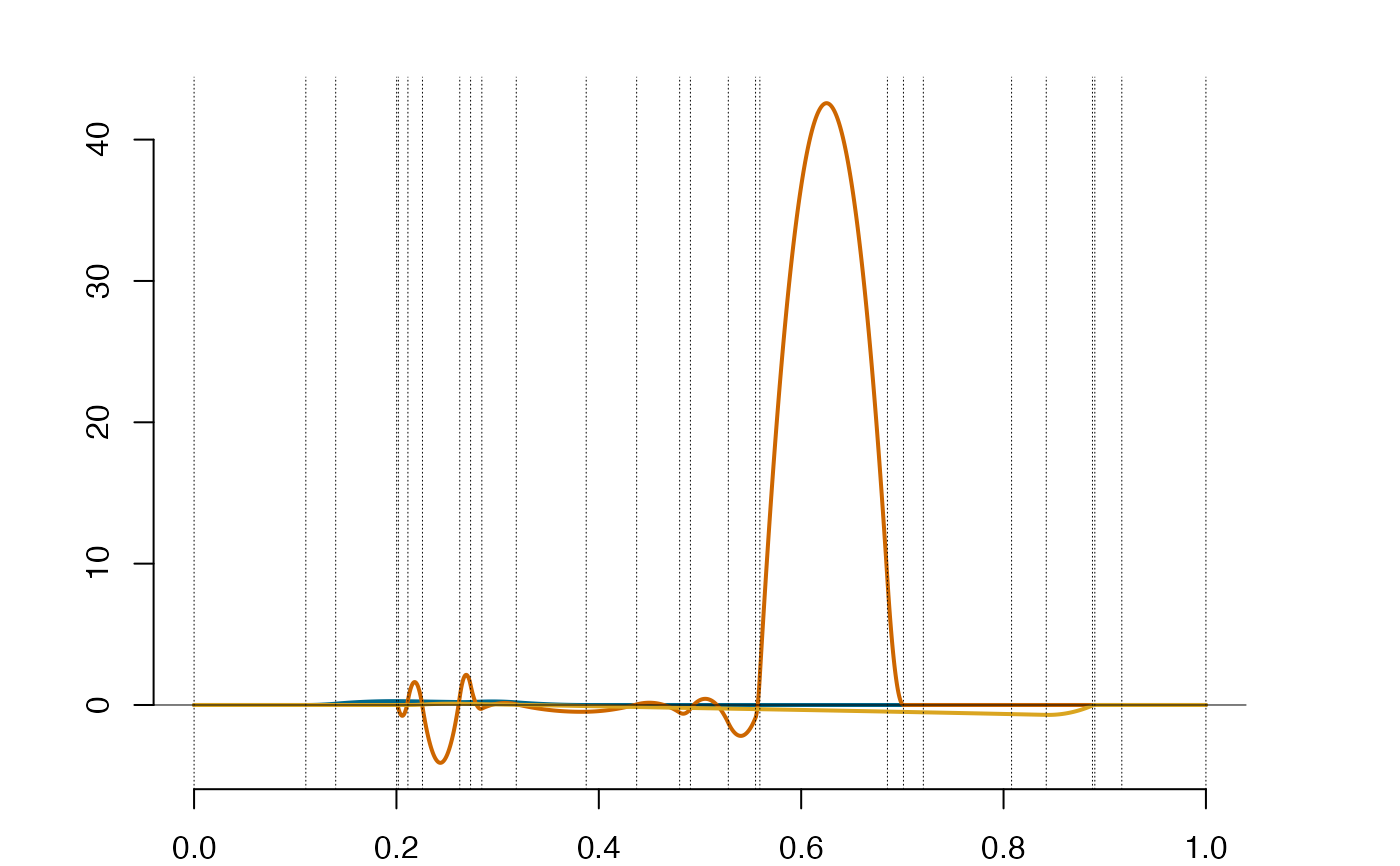 is.splinets(idspl) #and confirms that the object is a spline with boundary conditions
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 27 non-equaly distributed knots between 0 and 1
#> Size: 3 spline functions
#> Order: 2
#> Support: Not the full range support, a single support interval for each spline.
#> $Er
#> [1] 1.481881e-22
#>
#satified
idspl@supp #Since integral is taken over a function that integrates to zero over
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
spl@supp #each of the support interval, the support of all three objects are the same.
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
dspl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
ispl=integra(spl)
plot(ispl) #the zero boundary condition at the RHS-end for the splines are not satisfied.
is.splinets(idspl) #and confirms that the object is a spline with boundary conditions
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 27 non-equaly distributed knots between 0 and 1
#> Size: 3 spline functions
#> Order: 2
#> Support: Not the full range support, a single support interval for each spline.
#> $Er
#> [1] 1.481881e-22
#>
#satified
idspl@supp #Since integral is taken over a function that integrates to zero over
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
spl@supp #each of the support interval, the support of all three objects are the same.
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
dspl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
ispl=integra(spl)
plot(ispl) #the zero boundary condition at the RHS-end for the splines are not satisfied.
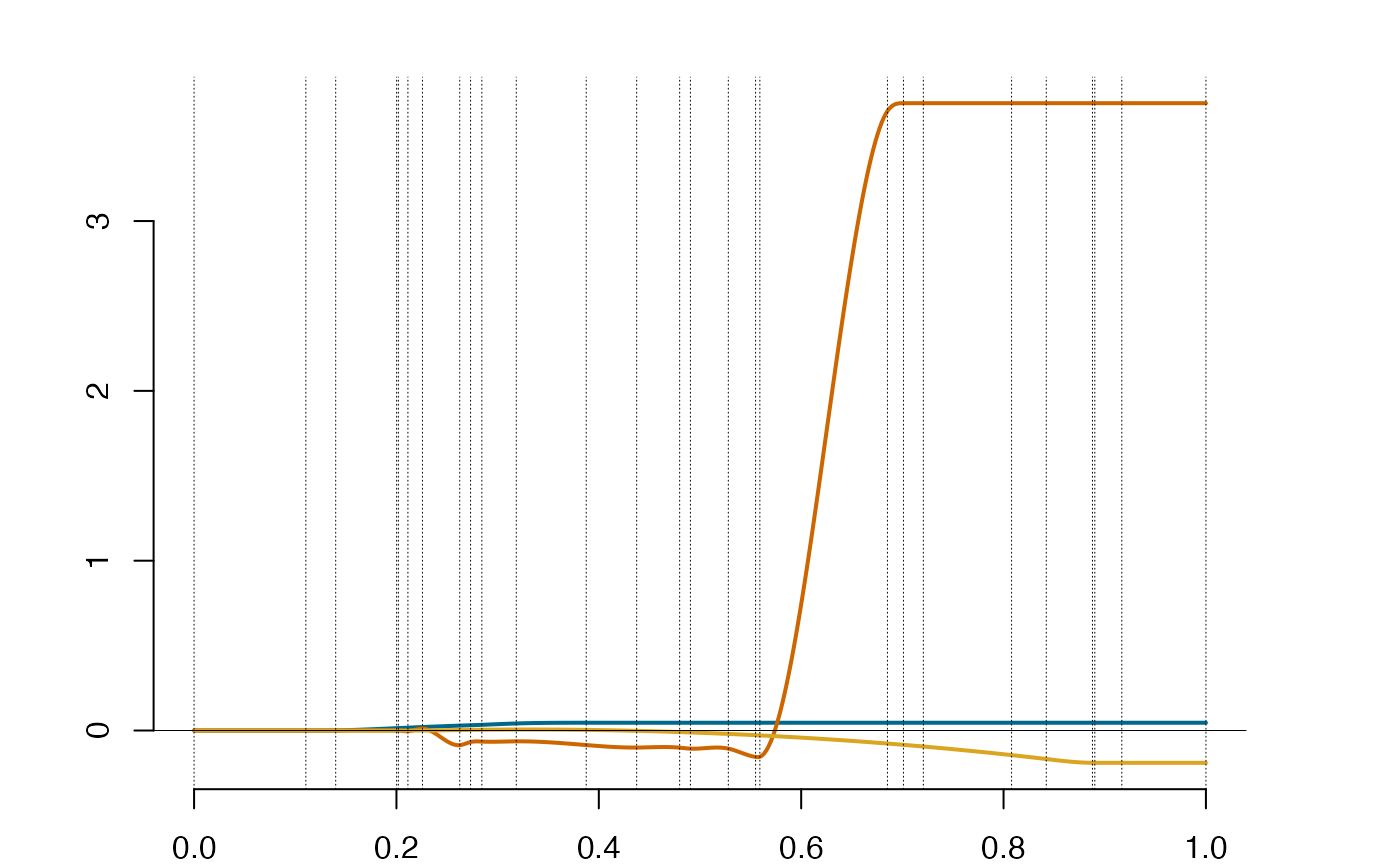 is.splinets(ispl) #thus the object is reported as a non-spline
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 2 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 3 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.005288035 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The derivative matrix for spline 2 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.4265515 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The derivative matrix for spline 3 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.02196226 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#> $is
#> [1] FALSE
#>
#> $robject
#> splines
#> Knots: 27 non-equaly distributed knots between 0 and 1
#> Size: 3 spline functions
#> Order: 3
#> Support: The full support range for each spline.
#> $Er
#> [1] 13.68423
#>
plot(deriva(ispl))
is.splinets(ispl) #thus the object is reported as a non-spline
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 2 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 3 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.005288035 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The derivative matrix for spline 2 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.4265515 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The derivative matrix for spline 3 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 0.02196226 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#> $is
#> [1] FALSE
#>
#> $robject
#> splines
#> Knots: 27 non-equaly distributed knots between 0 and 1
#> Size: 3 spline functions
#> Order: 3
#> Support: The full support range for each spline.
#> $Er
#> [1] 13.68423
#>
plot(deriva(ispl))
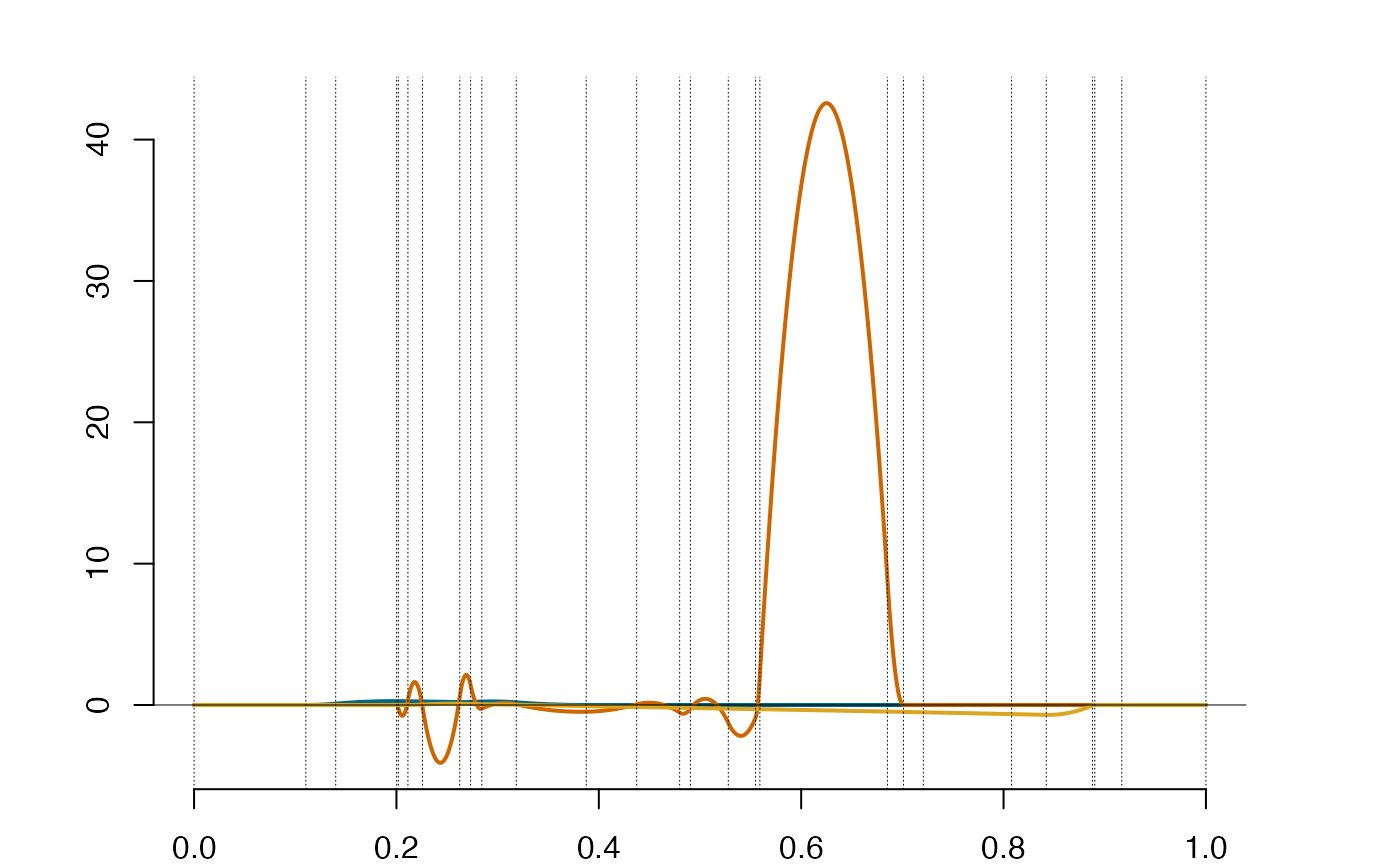 displ=deriva(ispl)
displ@supp #Comparison of the supports
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
spl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
#Here the integrals have extended support as it is taken from a function
ispl@supp #that does not integrate to zero.
#> list()
#---------------------------------------#
#---Example with complicated supports---#
#---------------------------------------#
n=40; xi=seq(0,1,by=1/(n+1)); k=3;
support=list(matrix(c(2,12,15,27,30,40),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp1 = is.splinets(sp)[[2]] #Comparison of the corrected and the original 'der' matrices
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 1 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.660117 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 support 2 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 2 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.375712 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 support 3 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 3 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.494706 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
support=list(matrix(c(2,13,17,30),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp2 = is.splinets(sp)[[2]]
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.679842 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.292027 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
sp = gather(sp1,sp2) #a group of two splines
plot(sp)
displ=deriva(ispl)
displ@supp #Comparison of the supports
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
spl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 4 20
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 6 25
#>
#Here the integrals have extended support as it is taken from a function
ispl@supp #that does not integrate to zero.
#> list()
#---------------------------------------#
#---Example with complicated supports---#
#---------------------------------------#
n=40; xi=seq(0,1,by=1/(n+1)); k=3;
support=list(matrix(c(2,12,15,27,30,40),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp1 = is.splinets(sp)[[2]] #Comparison of the corrected and the original 'der' matrices
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 1 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.660117 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 support 2 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 2 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.375712 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 support 3 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 3 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.494706 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
support=list(matrix(c(2,13,17,30),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp2 = is.splinets(sp)[[2]]
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.679842 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.292027 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
sp = gather(sp1,sp2) #a group of two splines
plot(sp)
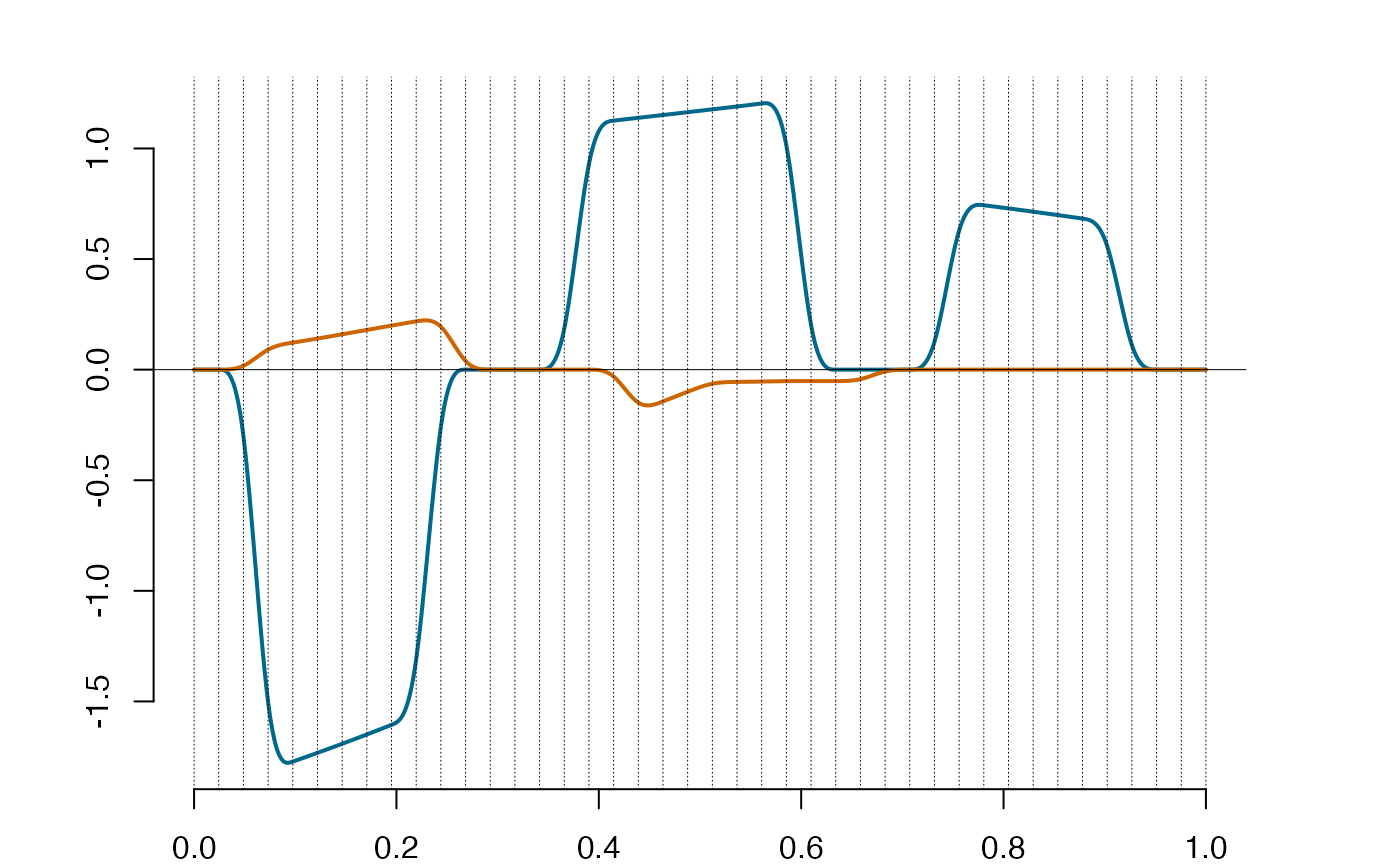 dsp = deriva(sp) #derivative
plot(dsp)
dsp = deriva(sp) #derivative
plot(dsp)
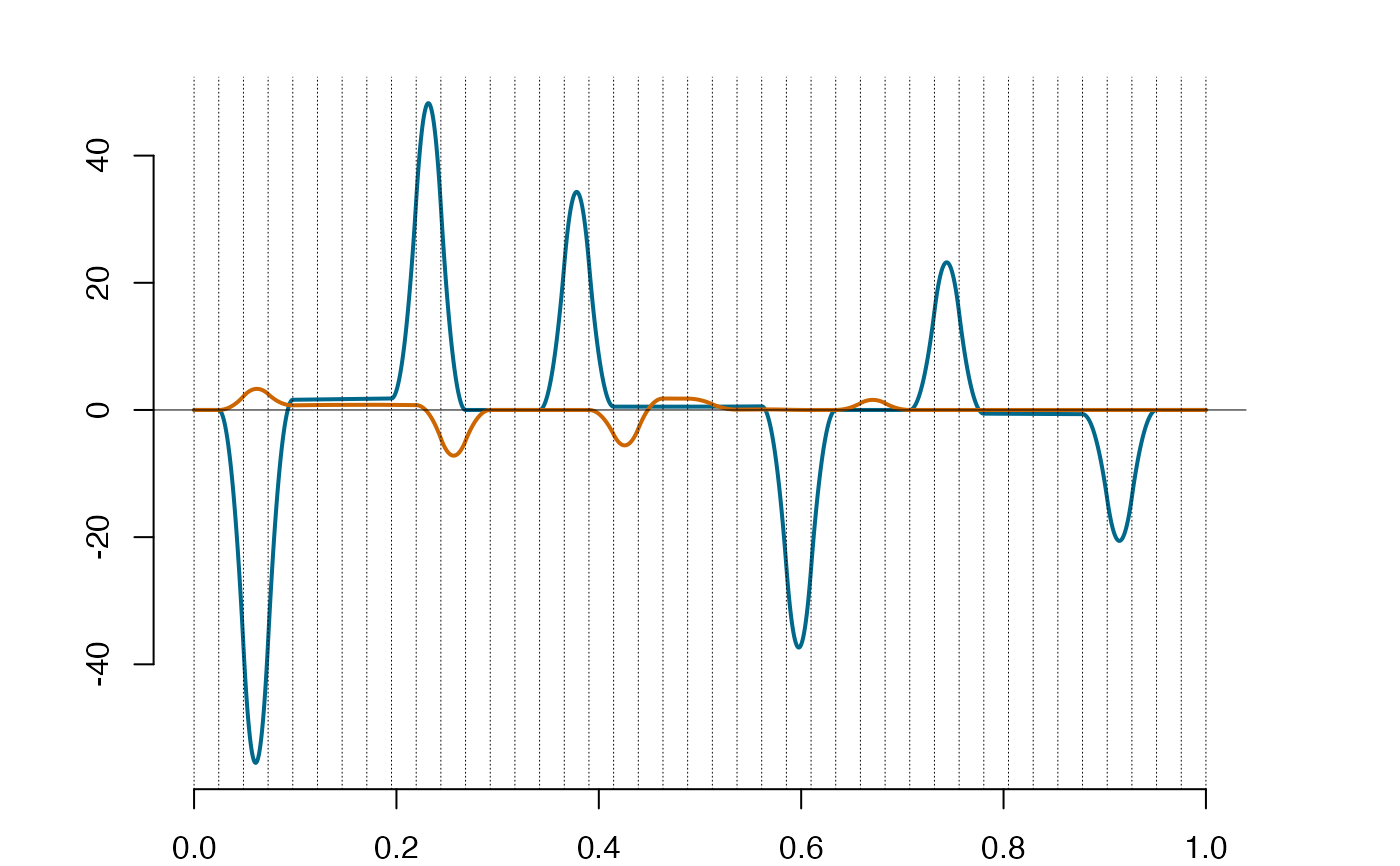 spl = integra(dsp)
plot(spl) #the spline retrieved
spl = integra(dsp)
plot(spl) #the spline retrieved
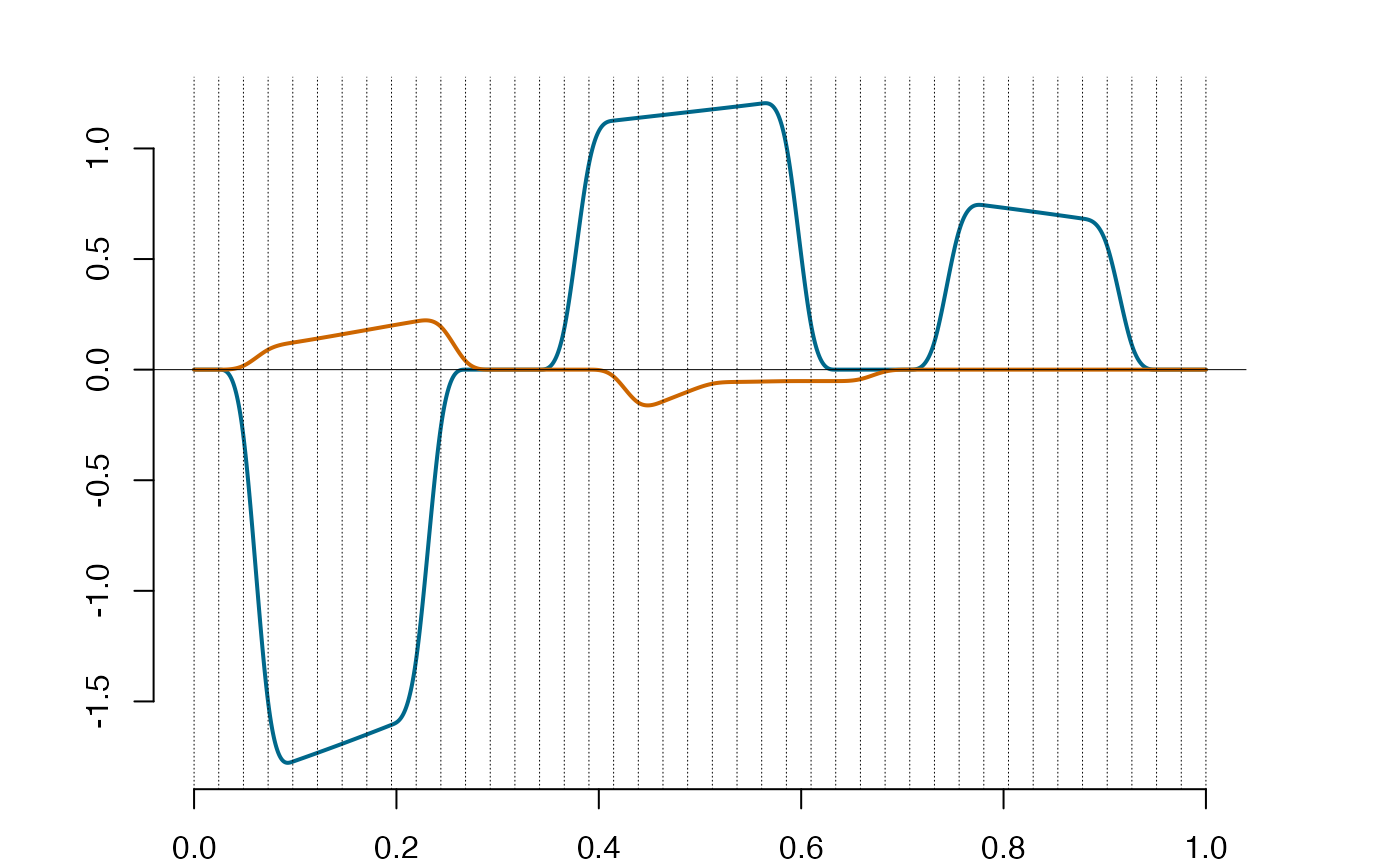 spl@supp #the supports are retrieved as well
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 15 27
#> [3,] 30 40
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 13
#> [2,] 17 30
#>
sp@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 15 27
#> [3,] 30 40
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 13
#> [2,] 17 30
#>
is.splinets(spl) #the proper splinet object that satisfies the boundaries
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 42 equaly distributed knots between 0 and 1
#> Size: 2 spline functions
#> Order: 3
#> Support: Not the full range support, the number of support intervals varies from 2 to 3
#> $Er
#> [1] 1.220483e-21
#>
ispl = integra(sp)
plot(ispl)
spl@supp #the supports are retrieved as well
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 15 27
#> [3,] 30 40
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 13
#> [2,] 17 30
#>
sp@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 15 27
#> [3,] 30 40
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 13
#> [2,] 17 30
#>
is.splinets(spl) #the proper splinet object that satisfies the boundaries
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 42 equaly distributed knots between 0 and 1
#> Size: 2 spline functions
#> Order: 3
#> Support: Not the full range support, the number of support intervals varies from 2 to 3
#> $Er
#> [1] 1.220483e-21
#>
ispl = integra(sp)
plot(ispl)
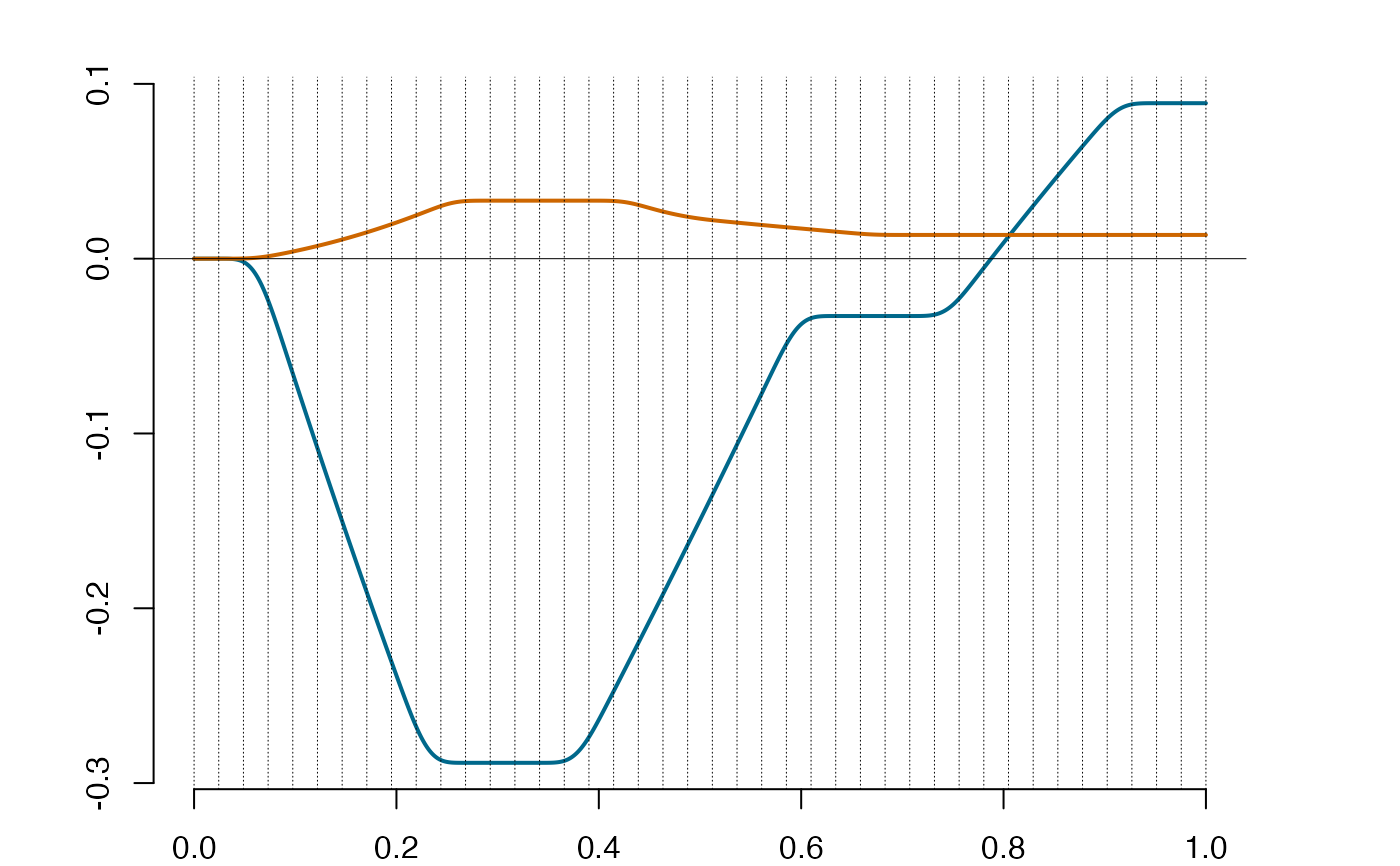 ispl@supp #full support shown by empty list in SLOT 'supp'
#> list()
is.splinets(ispl) #diagnostic confirms no zeros at the boundaries
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 2 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The matrix of derivatives at the knots for spline 1 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 0.007032306 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> The matrix of derivatives at the knots for spline 2 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 0.001073566 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 2 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> $is
#> [1] FALSE
#>
#> $robject
#> splines
#> Knots: 42 equaly distributed knots between 0 and 1
#> Size: 2 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 0.008096939
#>
spll = deriva(ispl)
plot(spll)
ispl@supp #full support shown by empty list in SLOT 'supp'
#> list()
is.splinets(ispl) #diagnostic confirms no zeros at the boundaries
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 2 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The matrix of derivatives at the knots for spline 1 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 0.007032306 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> The matrix of derivatives at the knots for spline 2 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 0.001073566 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 2 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> $is
#> [1] FALSE
#>
#> $robject
#> splines
#> Knots: 42 equaly distributed knots between 0 and 1
#> Size: 2 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 0.008096939
#>
spll = deriva(ispl)
plot(spll)
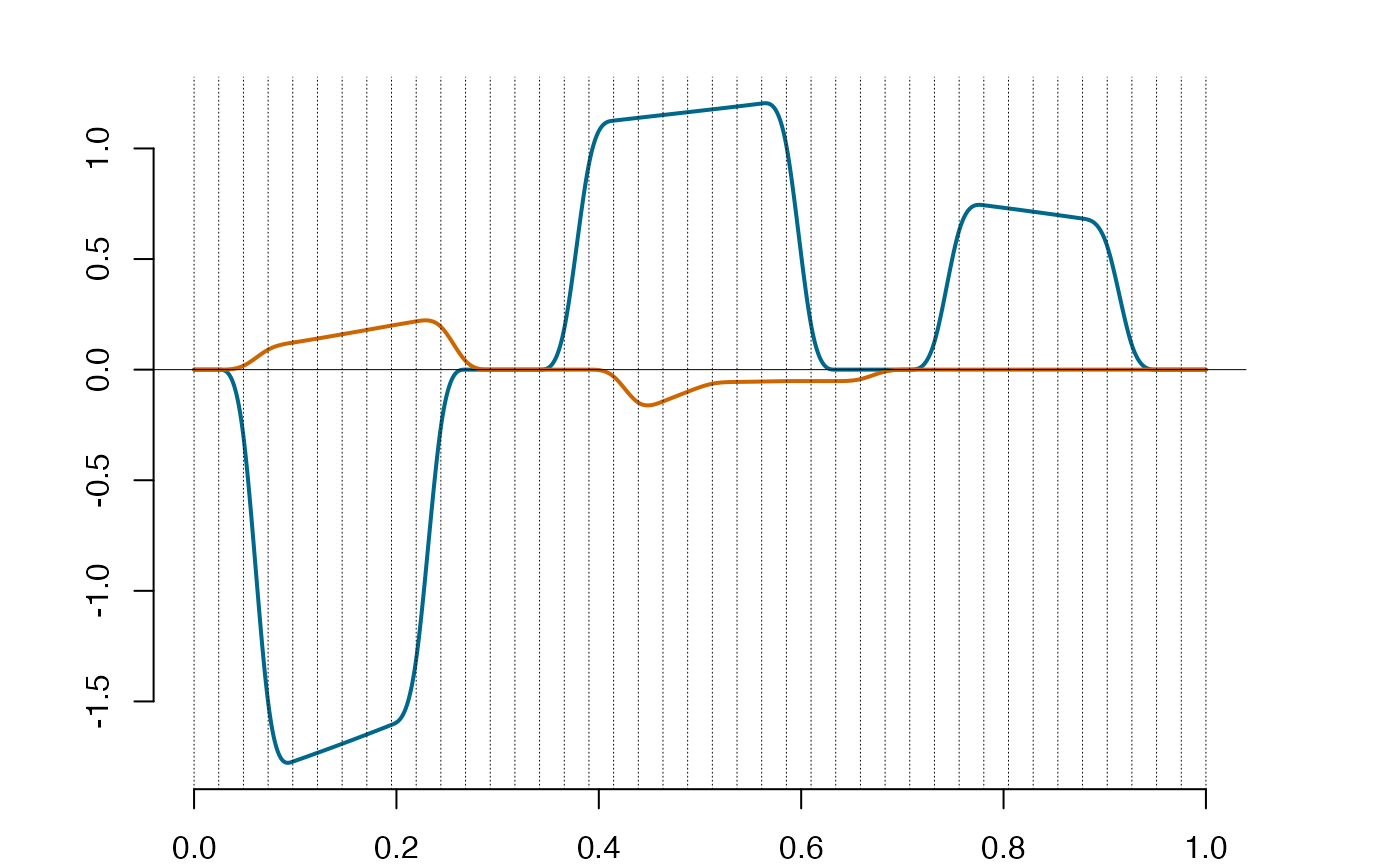 spll@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 15 27
#> [3,] 30 40
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 13
#> [2,] 17 30
#>
spll@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 2 12
#> [2,] 15 27
#> [3,] 30 40
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 2 13
#> [2,] 17 30
#>