The function performs evaluation of the matrix of the inner products \(\int S(t) \cdot T(t) dt \) of all the pairs of splines \(S\), \(T\) from the input object. The program utilizes the Taylor expansion of splines, see the reference for details.
Arguments
- Sp
Splinetsobject;- norm_only
logical, indicates if only the square norm of the elements in the input object is calculated; The default is
norm_only=FALSE;- sID
vector of integers, the indicies specifying splines in the
SplinetslistSpto be evaluated; IfsID=NULL(default), then the inner products for all the pairs taken from the object are evaluated.- Sp2
Splinetsobject, the optional secondSplinets-object; The inner products between splines inSpand inSp2are evaluated, i.e. the cross-gramian matrix.- s2ID
vector of integers, the indicies specifying splines in the
Sp2to be considered in the cross-gramian;
Value
norm_only=FALSE– the Gram matrix of inner products of the splines within the inputSplinets-objects is returned,Sp2 = NULL– the non-negative definite matrix of the inner products of splines inSpis returned,both
SpandSp2are non-NULLand contain splines \(S_i\)'s and \(T_j\)'s, respectively == the cross-gramian matris of the inner products for the pairs of splines \((S_i,T_j)\) is returned,norm_only=FALSE– the vector of the norms ofSpis returned.
Details
If there is only one input Splinet-object, then the non-negative symmetrix matrix of the splines in this object is returned.
If there are two input Splinet-objects, then the \(m \times r\) matrix of the cross-inner product is returned, where \(m\) is
the number of splines in the first object and \(r\) is their number in the second one.
If only the norms are evaluated (norm_only= TRUE) it is always evaluating the norms of the first object.
In the case of two input Splinets-objects, they should be over the same set of knots and of the same smoothness order.
References
Liu, X., Nassar, H., Podg\(\mbox{\'o}\)rski, K. "Dyadic diagonalization of positive definite band matrices and efficient B-spline orthogonalization." Journal of Computational and Applied Mathematics (2022) <https://doi.org/10.1016/j.cam.2022.114444>.
Podg\(\mbox{\'o}\)rski, K. (2021)
"Splinets – splines through the Taylor expansion, their support sets and orthogonal bases." <arXiv:2102.00733>.
Nassar, H., Podg\(\mbox{\'o}\)rski, K. (2023) "Splinets 1.5.0 – Periodic Splinets." <arXiv:2302.07552>
Examples
#---------------------------------------#
#---- Simple three splines example -----#
#---------------------------------------#
n=25; k=3
xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
#Defining support ranges for three splines
supp=matrix(c(2,12,4,20,6,25),byrow=TRUE,ncol=2)
#Initial random matrices of the derivative for each spline
SS1=matrix(rnorm((supp[1,2]-supp[1,1]+1)*(k+1)),ncol=(k+1))
SS2=matrix(rnorm((supp[2,2]-supp[2,1]+1)*(k+1)),ncol=(k+1))
SS3=matrix(rnorm((supp[3,2]-supp[3,1]+1)*(k+1)),ncol=(k+1))
spl=construct(xi,k,SS1,supp[1,]) #constructing the first correct spline
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.418853 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
nspl=construct(xi,k,SS2,supp[2,])
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 support 1 's highest derivative at the central knot is not zero.
#> Now it is set to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.291063 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl,nspl) #the second and the first ones
nspl=construct(xi,k,SS3,supp[3,])
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 - highest derivative is not symmetric at the center (equal values at the two central knots).
#> The two values have been made equal by averaging.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the splie conditions (up to the accuracy set in SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.476759 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> There are less than 5 knots, the first 2 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 5 knots, the first 2 entries of the 5 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> The matrix derivative is now corrected by method RRM .
spl=gather(spl,nspl) #the third is added
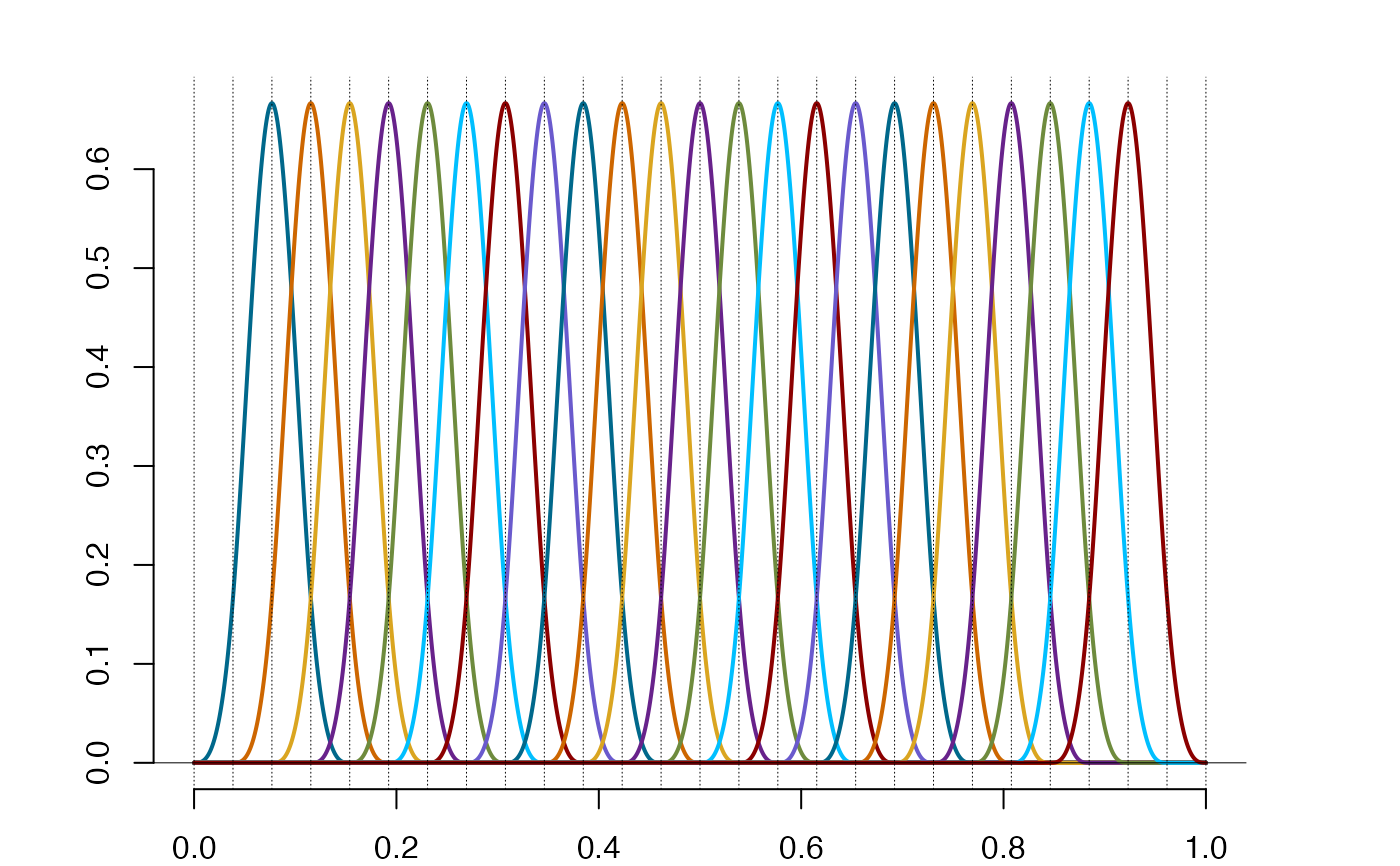
plot(spl)
 gramian(spl)
#> [,1] [,2] [,3]
#> [1,] 0.6529948 0.24933900 -0.10598721
#> [2,] 0.2493390 0.21677143 -0.02862501
#> [3,] -0.1059872 -0.02862501 0.43189486
gramian(spl, norm_only = TRUE)
#> [1] 0.6529948 0.2167714 0.4318949
gramian(spl, sID = c(1,3))
#> [,1] [,2]
#> [1,] 0.6529948 -0.1059872
#> [2,] -0.1059872 0.4318949
gramian(spl,sID=c(2,3),Sp2=spl,s2ID=c(1)) #the cross-Gramian matrix
#> [,1]
#> [1,] 0.2493390
#> [2,] -0.1059872
#-----------------------------------------#
#--- Example with varying support sets ---#
#-----------------------------------------#
n=40; xi=seq(0,1,by=1/(n+1)); k=2;
support=list(matrix(c(2,9,15,24,30,37),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp1 = is.splinets(sp)[[2]] #the correction of 'der' matrices
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.613142 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.457952 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 3 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 3 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.458022 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
support=list(matrix(c(5,12,17,29),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp2 = is.splinets(sp)[[2]]
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.546269 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 support 2 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 2 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.853498 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
spp = gather(sp1,sp2)
support=list(matrix(c(3,10,14,21,27,34),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp3 = is.splinets(sp)[[2]]
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.432885 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 0.8928797 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 3 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 3 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.216008 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
spp = gather(spp, sp3)
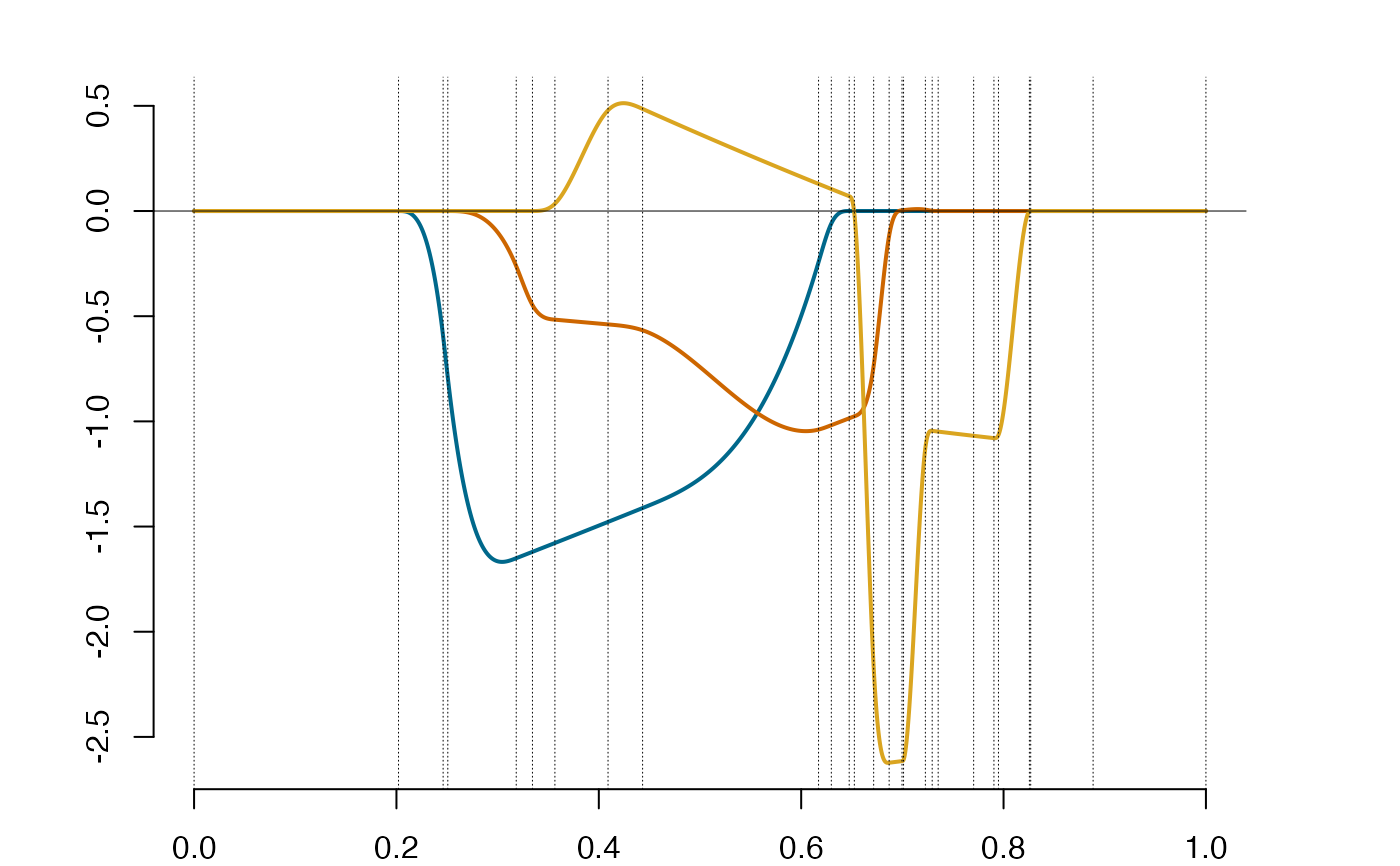
plot(spp)
gramian(spl)
#> [,1] [,2] [,3]
#> [1,] 0.6529948 0.24933900 -0.10598721
#> [2,] 0.2493390 0.21677143 -0.02862501
#> [3,] -0.1059872 -0.02862501 0.43189486
gramian(spl, norm_only = TRUE)
#> [1] 0.6529948 0.2167714 0.4318949
gramian(spl, sID = c(1,3))
#> [,1] [,2]
#> [1,] 0.6529948 -0.1059872
#> [2,] -0.1059872 0.4318949
gramian(spl,sID=c(2,3),Sp2=spl,s2ID=c(1)) #the cross-Gramian matrix
#> [,1]
#> [1,] 0.2493390
#> [2,] -0.1059872
#-----------------------------------------#
#--- Example with varying support sets ---#
#-----------------------------------------#
n=40; xi=seq(0,1,by=1/(n+1)); k=2;
support=list(matrix(c(2,9,15,24,30,37),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp1 = is.splinets(sp)[[2]] #the correction of 'der' matrices
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.613142 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.457952 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 3 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 3 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.458022 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
support=list(matrix(c(5,12,17,29),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp2 = is.splinets(sp)[[2]]
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.546269 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 support 2 's highest derivative at the central knot is not equal to zero.
#> Spline 1 support 2 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.853498 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
spp = gather(sp1,sp2)
support=list(matrix(c(3,10,14,21,27,34),ncol=2,byrow = TRUE))
sp=new("Splinets",knots=xi,smorder=k,supp=support)
m=sum(sp@supp[[1]][,2]-sp@supp[[1]][,1]+1) #the number of knots in the support
sp@der=list(matrix(rnorm(m*(k+1)),ncol=(k+1))) #the derivative matrix at random
sp3 = is.splinets(sp)[[2]]
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 1 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 2 of spline 1 in the output 'Splinets' object.
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices over the support component 3 of spline 1 in the output 'Splinets' object.
#>
#> Spline 1 , support 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 1 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 1 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.432885 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 1 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 2 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 2 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 2 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 0.8928797 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 2 has the derivative matrix corrected by the RRM method.
#> Spline 1 , support 3 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 highest, support 3 's derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 , support 3 does not satisfy the conditions that are required for a spline (up to the accuracy SLOT 'epsilon').
#> The computed standard error per matrix entry is 1.216008 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 support 3 has the derivative matrix corrected by the RRM method.
spp = gather(spp, sp3)
plot(spp)
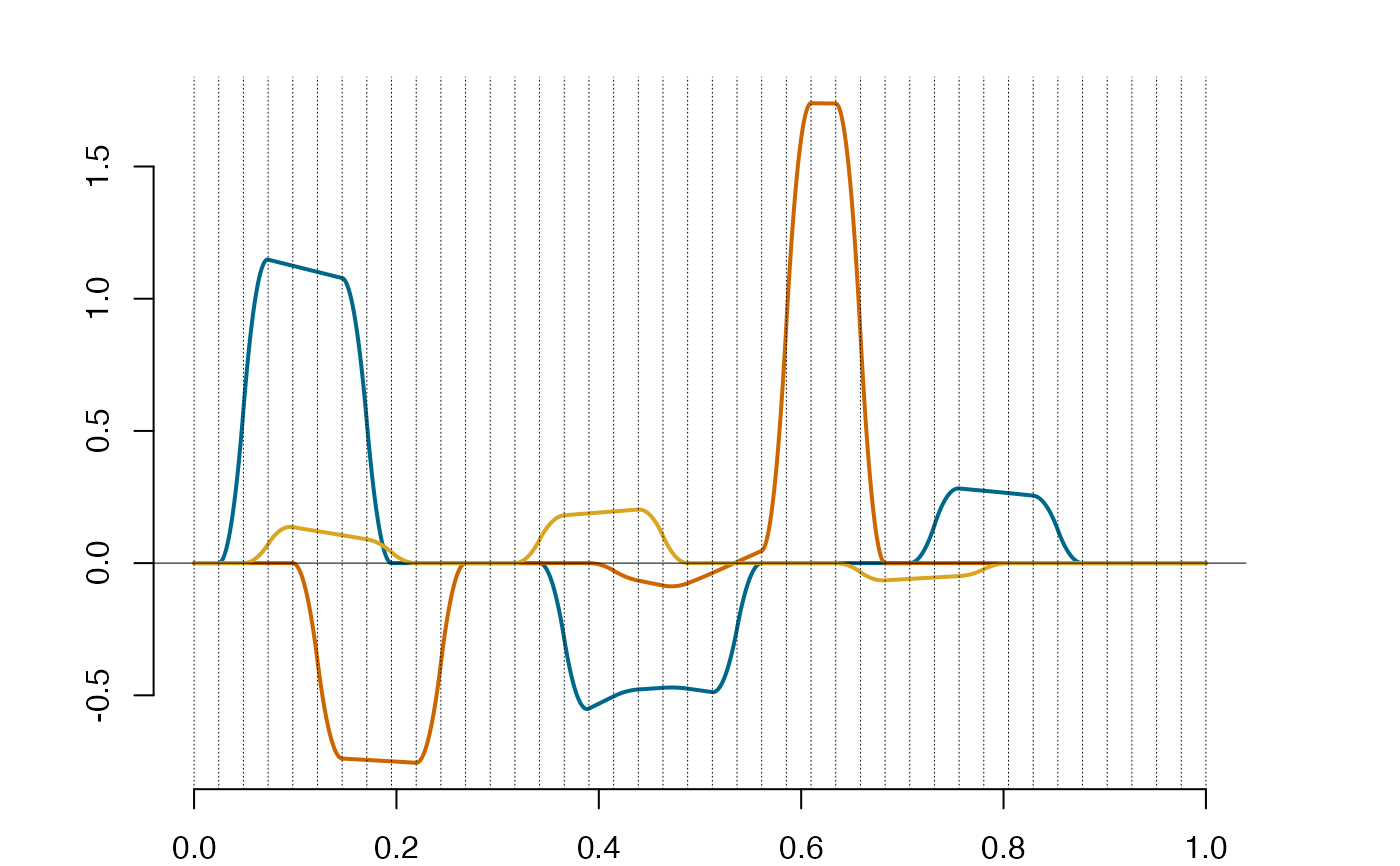 gramian(spp) #the regular gramian matrix
#> [,1] [,2] [,3]
#> [1,] 0.184674517 -0.035625141 0.002490996
#> [2,] -0.035625141 0.250416141 -0.006716441
#> [3,] 0.002490996 -0.006716441 0.005898704
spp2=subsample(spp,sample(1:3,size=3,rep=TRUE))
gramian(Sp=spp,Sp2=spp2) #cross-Gramian matrix
#> [,1] [,2] [,3]
#> [1,] -0.035625141 0.184674517 -0.035625141
#> [2,] 0.250416141 -0.035625141 0.250416141
#> [3,] -0.006716441 0.002490996 -0.006716441
#-----------------------------------------#
#--------- Grammian for B-splines --------#
#-----------------------------------------#
n=25; xi=seq(0,1,by=1/(n+1)); k=2;
Sp=splinet(xi) #B-splines and corresponding splinet
gramian(Sp$bs) #band grammian matrix for B-splines
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [2,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [3,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [4,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [5,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [6,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [13,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,6] [,7] [,8] [,9] [,10]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00
#> [6,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [7,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [8,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [9,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [10,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [11,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [13,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,11] [,12] [,13] [,14] [,15]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00
#> [11,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [12,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [13,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [14,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [15,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [16,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,16] [,17] [,18] [,19] [,20]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [13,] 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [14,] 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00
#> [16,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [17,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [18,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [19,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [20,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [21,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [,21] [,22] [,23]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [13,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 7.631258e-06 0.000000e+00 0.000000e+00
#> [19,] 9.157509e-04 7.631258e-06 0.000000e+00
#> [20,] 9.088828e-03 9.157509e-04 7.631258e-06
#> [21,] 1.843712e-02 9.088828e-03 9.157509e-04
#> [22,] 9.088828e-03 1.843712e-02 9.088828e-03
#> [23,] 9.157509e-04 9.088828e-03 1.843712e-02
gramian(Sp$os) #diagonal gramian matrix for the splinet
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.000000e+00 -5.596038e-16 -2.609887e-16 -3.798495e-16 1.043450e-16
#> [2,] -5.596038e-16 1.000000e+00 3.814427e-16 3.238809e-17 2.043698e-17
#> [3,] -2.609887e-16 3.814427e-16 1.000000e+00 -8.477328e-16 2.187079e-16
#> [4,] -3.798495e-16 3.238809e-17 -8.477328e-16 1.000000e+00 -5.761791e-16
#> [5,] 1.043450e-16 2.043698e-17 2.187079e-16 -5.761791e-16 1.000000e+00
#> [6,] 5.528522e-16 -3.188186e-17 -6.221949e-16 2.516825e-16 -5.536149e-16
#> [7,] -1.364130e-17 -8.591478e-19 -4.894808e-17 4.110375e-17 -2.269577e-17
#> [8,] -1.956173e-17 0.000000e+00 0.000000e+00 0.000000e+00 4.364782e-18
#> [9,] 1.077349e-17 0.000000e+00 0.000000e+00 0.000000e+00 -2.044905e-17
#> [10,] -2.139122e-18 0.000000e+00 0.000000e+00 0.000000e+00 -4.452504e-18
#> [11,] 4.329480e-18 -2.849605e-18 -6.941719e-19 -3.540586e-17 -2.260428e-17
#> [12,] 9.981672e-18 -3.958199e-18 1.834303e-17 4.468800e-18 6.018597e-18
#> [13,] -1.629385e-19 8.843864e-20 -5.010109e-19 3.526881e-19 -3.690355e-19
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,6] [,7] [,8] [,9] [,10]
#> [1,] 5.528522e-16 -1.364130e-17 -1.956173e-17 1.077349e-17 -2.139122e-18
#> [2,] -3.188186e-17 -8.591478e-19 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] -6.221949e-16 -4.894808e-17 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 2.516825e-16 4.110375e-17 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] -5.536149e-16 -2.269577e-17 4.364782e-18 -2.044905e-17 -4.452504e-18
#> [6,] 1.000000e+00 8.738147e-16 -3.272195e-16 -3.536276e-17 -2.791678e-17
#> [7,] 8.738147e-16 1.000000e+00 -4.017155e-16 7.103781e-16 -5.688212e-17
#> [8,] -3.272195e-16 -4.017155e-16 1.000000e+00 2.458533e-17 6.615055e-18
#> [9,] -3.536276e-17 7.103781e-16 2.458533e-17 1.000000e+00 -2.529704e-16
#> [10,] -2.791678e-17 -5.688212e-17 6.615055e-18 -2.529704e-16 1.000000e+00
#> [11,] -2.718100e-16 3.025570e-16 -7.113632e-18 1.087077e-15 -1.400184e-15
#> [12,] 5.664200e-17 -1.267454e-16 2.024615e-17 -5.402578e-16 1.718297e-16
#> [13,] 7.937923e-19 6.642628e-18 -1.432033e-18 -4.806067e-17 2.298509e-17
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,11] [,12] [,13] [,14] [,15]
#> [1,] 4.329480e-18 9.981672e-18 -1.629385e-19 0.000000e+00 0.000000e+00
#> [2,] -2.849605e-18 -3.958199e-18 8.843864e-20 0.000000e+00 0.000000e+00
#> [3,] -6.941719e-19 1.834303e-17 -5.010109e-19 0.000000e+00 0.000000e+00
#> [4,] -3.540586e-17 4.468800e-18 3.526881e-19 0.000000e+00 0.000000e+00
#> [5,] -2.260428e-17 6.018597e-18 -3.690355e-19 0.000000e+00 0.000000e+00
#> [6,] -2.718100e-16 5.664200e-17 7.937923e-19 0.000000e+00 0.000000e+00
#> [7,] 3.025570e-16 -1.267454e-16 6.642628e-18 0.000000e+00 0.000000e+00
#> [8,] -7.113632e-18 2.024615e-17 -1.432033e-18 0.000000e+00 0.000000e+00
#> [9,] 1.087077e-15 -5.402578e-16 -4.806067e-17 0.000000e+00 0.000000e+00
#> [10,] -1.400184e-15 1.718297e-16 2.298509e-17 0.000000e+00 0.000000e+00
#> [11,] 1.000000e+00 -2.437609e-15 -2.325477e-16 -6.938885e-18 -4.112178e-17
#> [12,] -2.437609e-15 1.000000e+00 2.939043e-15 -4.150024e-16 -1.222252e-15
#> [13,] -2.325477e-16 2.939043e-15 1.000000e+00 -8.767934e-16 6.588478e-16
#> [14,] -6.938885e-18 -4.150024e-16 -8.767934e-16 1.000000e+00 -2.688308e-16
#> [15,] -4.112178e-17 -1.222252e-15 6.588478e-16 -2.688308e-16 1.000000e+00
#> [16,] 2.656958e-18 1.808320e-16 -5.469462e-17 3.040555e-17 1.118171e-16
#> [17,] -8.969883e-18 -1.901868e-16 5.880429e-16 -2.095378e-16 5.041938e-16
#> [18,] 2.507992e-17 -3.058981e-17 -5.969468e-16 1.088786e-16 -1.193167e-15
#> [19,] -2.475485e-18 -3.164968e-17 3.786323e-17 5.088476e-18 -4.002665e-17
#> [20,] 1.467867e-18 1.413369e-17 -2.797133e-17 0.000000e+00 0.000000e+00
#> [21,] -1.771076e-18 -5.199643e-18 1.318362e-17 0.000000e+00 0.000000e+00
#> [22,] 4.003676e-20 -6.498330e-18 1.363294e-18 0.000000e+00 0.000000e+00
#> [23,] -1.340072e-18 -8.852469e-18 4.329480e-18 6.488259e-19 3.456399e-17
#> [,16] [,17] [,18] [,19] [,20]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 2.656958e-18 -8.969883e-18 2.507992e-17 -2.475485e-18 1.467867e-18
#> [12,] 1.808320e-16 -1.901868e-16 -3.058981e-17 -3.164968e-17 1.413369e-17
#> [13,] -5.469462e-17 5.880429e-16 -5.969468e-16 3.786323e-17 -2.797133e-17
#> [14,] 3.040555e-17 -2.095378e-16 1.088786e-16 5.088476e-18 0.000000e+00
#> [15,] 1.118171e-16 5.041938e-16 -1.193167e-15 -4.002665e-17 0.000000e+00
#> [16,] 1.000000e+00 -1.400200e-16 4.499366e-16 -1.099991e-17 0.000000e+00
#> [17,] -1.400200e-16 1.000000e+00 -1.283190e-15 1.478028e-16 -6.848967e-18
#> [18,] 4.499366e-16 -1.283190e-15 1.000000e+00 -8.073802e-16 5.054478e-16
#> [19,] -1.099991e-17 1.478028e-16 -8.073802e-16 1.000000e+00 -7.665030e-16
#> [20,] 0.000000e+00 -6.848967e-18 5.054478e-16 -7.665030e-16 1.000000e+00
#> [21,] 0.000000e+00 -1.821870e-17 -1.161446e-15 5.200541e-16 -4.195039e-16
#> [22,] 0.000000e+00 -1.176312e-17 -1.191137e-16 1.611974e-16 -2.649931e-16
#> [23,] -2.823535e-17 5.178255e-17 -9.062980e-16 2.074371e-16 1.269364e-17
#> [,21] [,22] [,23]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] -1.771076e-18 4.003676e-20 -1.340072e-18
#> [12,] -5.199643e-18 -6.498330e-18 -8.852469e-18
#> [13,] 1.318362e-17 1.363294e-18 4.329480e-18
#> [14,] 0.000000e+00 0.000000e+00 6.488259e-19
#> [15,] 0.000000e+00 0.000000e+00 3.456399e-17
#> [16,] 0.000000e+00 0.000000e+00 -2.823535e-17
#> [17,] -1.821870e-17 -1.176312e-17 5.178255e-17
#> [18,] -1.161446e-15 -1.191137e-16 -9.062980e-16
#> [19,] 5.200541e-16 1.611974e-16 2.074371e-16
#> [20,] -4.195039e-16 -2.649931e-16 1.269364e-17
#> [21,] 1.000000e+00 1.118171e-16 8.650947e-16
#> [22,] 1.118171e-16 1.000000e+00 -2.661877e-16
#> [23,] 8.650947e-16 -2.661877e-16 1.000000e+00
A=gramian(Sp=Sp$bs,Sp2=Sp$os) #cross-Gramian matrix, the coefficients of
#the decomposition of the B-splines
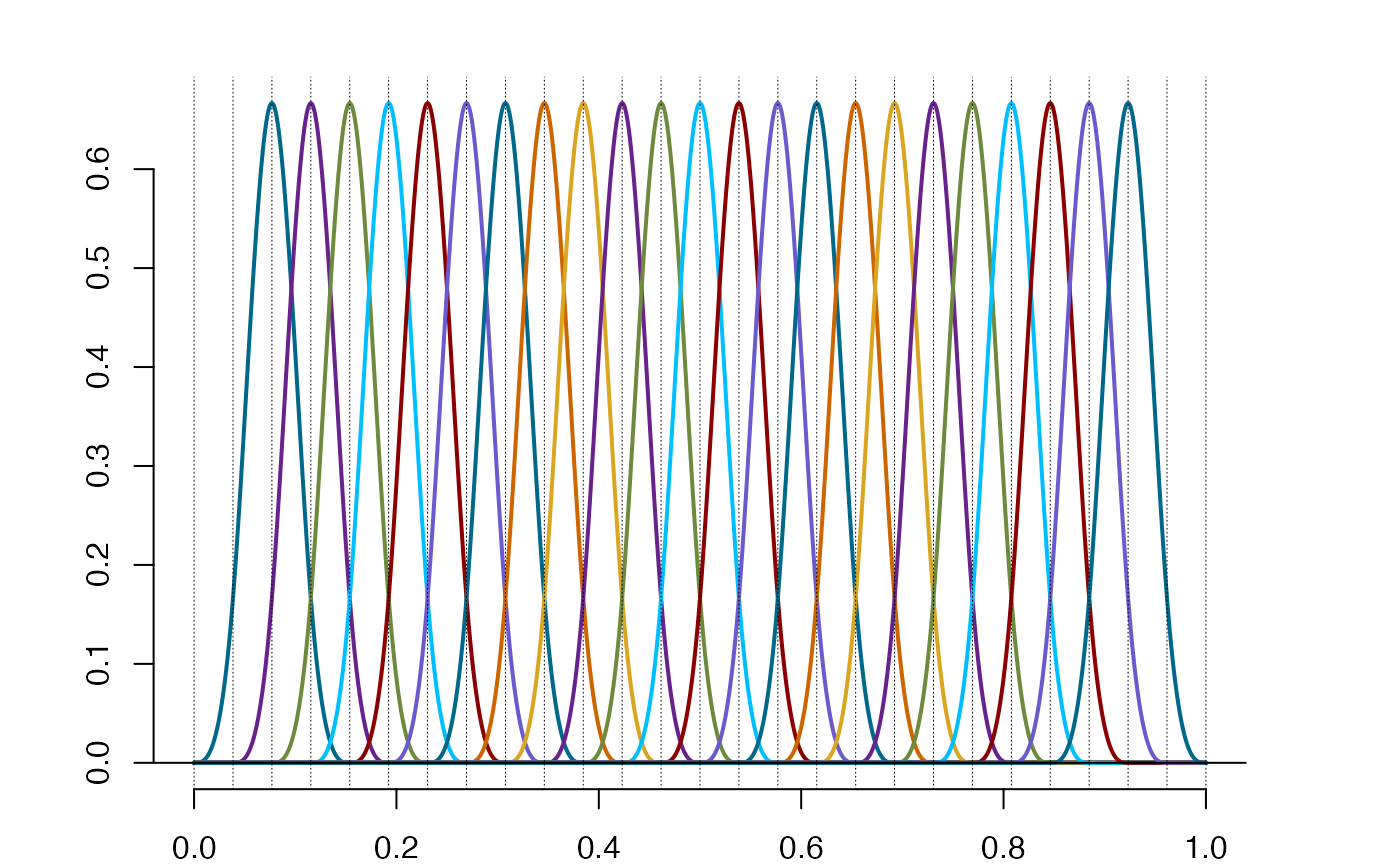
plot(Sp$bs)
gramian(spp) #the regular gramian matrix
#> [,1] [,2] [,3]
#> [1,] 0.184674517 -0.035625141 0.002490996
#> [2,] -0.035625141 0.250416141 -0.006716441
#> [3,] 0.002490996 -0.006716441 0.005898704
spp2=subsample(spp,sample(1:3,size=3,rep=TRUE))
gramian(Sp=spp,Sp2=spp2) #cross-Gramian matrix
#> [,1] [,2] [,3]
#> [1,] -0.035625141 0.184674517 -0.035625141
#> [2,] 0.250416141 -0.035625141 0.250416141
#> [3,] -0.006716441 0.002490996 -0.006716441
#-----------------------------------------#
#--------- Grammian for B-splines --------#
#-----------------------------------------#
n=25; xi=seq(0,1,by=1/(n+1)); k=2;
Sp=splinet(xi) #B-splines and corresponding splinet
gramian(Sp$bs) #band grammian matrix for B-splines
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [2,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [3,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [4,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [5,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [6,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [13,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,6] [,7] [,8] [,9] [,10]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00
#> [6,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [7,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [8,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [9,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [10,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [11,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [13,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,11] [,12] [,13] [,14] [,15]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00
#> [11,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [12,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [13,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [14,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [15,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [16,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,16] [,17] [,18] [,19] [,20]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [13,] 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [14,] 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00 0.000000e+00
#> [16,] 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06 0.000000e+00
#> [17,] 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04 7.631258e-06
#> [18,] 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03 9.157509e-04
#> [19,] 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02 9.088828e-03
#> [20,] 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03 1.843712e-02
#> [21,] 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04 9.088828e-03
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06 9.157509e-04
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 7.631258e-06
#> [,21] [,22] [,23]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [12,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [13,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 7.631258e-06 0.000000e+00 0.000000e+00
#> [19,] 9.157509e-04 7.631258e-06 0.000000e+00
#> [20,] 9.088828e-03 9.157509e-04 7.631258e-06
#> [21,] 1.843712e-02 9.088828e-03 9.157509e-04
#> [22,] 9.088828e-03 1.843712e-02 9.088828e-03
#> [23,] 9.157509e-04 9.088828e-03 1.843712e-02
gramian(Sp$os) #diagonal gramian matrix for the splinet
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.000000e+00 -5.596038e-16 -2.609887e-16 -3.798495e-16 1.043450e-16
#> [2,] -5.596038e-16 1.000000e+00 3.814427e-16 3.238809e-17 2.043698e-17
#> [3,] -2.609887e-16 3.814427e-16 1.000000e+00 -8.477328e-16 2.187079e-16
#> [4,] -3.798495e-16 3.238809e-17 -8.477328e-16 1.000000e+00 -5.761791e-16
#> [5,] 1.043450e-16 2.043698e-17 2.187079e-16 -5.761791e-16 1.000000e+00
#> [6,] 5.528522e-16 -3.188186e-17 -6.221949e-16 2.516825e-16 -5.536149e-16
#> [7,] -1.364130e-17 -8.591478e-19 -4.894808e-17 4.110375e-17 -2.269577e-17
#> [8,] -1.956173e-17 0.000000e+00 0.000000e+00 0.000000e+00 4.364782e-18
#> [9,] 1.077349e-17 0.000000e+00 0.000000e+00 0.000000e+00 -2.044905e-17
#> [10,] -2.139122e-18 0.000000e+00 0.000000e+00 0.000000e+00 -4.452504e-18
#> [11,] 4.329480e-18 -2.849605e-18 -6.941719e-19 -3.540586e-17 -2.260428e-17
#> [12,] 9.981672e-18 -3.958199e-18 1.834303e-17 4.468800e-18 6.018597e-18
#> [13,] -1.629385e-19 8.843864e-20 -5.010109e-19 3.526881e-19 -3.690355e-19
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,6] [,7] [,8] [,9] [,10]
#> [1,] 5.528522e-16 -1.364130e-17 -1.956173e-17 1.077349e-17 -2.139122e-18
#> [2,] -3.188186e-17 -8.591478e-19 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] -6.221949e-16 -4.894808e-17 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 2.516825e-16 4.110375e-17 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] -5.536149e-16 -2.269577e-17 4.364782e-18 -2.044905e-17 -4.452504e-18
#> [6,] 1.000000e+00 8.738147e-16 -3.272195e-16 -3.536276e-17 -2.791678e-17
#> [7,] 8.738147e-16 1.000000e+00 -4.017155e-16 7.103781e-16 -5.688212e-17
#> [8,] -3.272195e-16 -4.017155e-16 1.000000e+00 2.458533e-17 6.615055e-18
#> [9,] -3.536276e-17 7.103781e-16 2.458533e-17 1.000000e+00 -2.529704e-16
#> [10,] -2.791678e-17 -5.688212e-17 6.615055e-18 -2.529704e-16 1.000000e+00
#> [11,] -2.718100e-16 3.025570e-16 -7.113632e-18 1.087077e-15 -1.400184e-15
#> [12,] 5.664200e-17 -1.267454e-16 2.024615e-17 -5.402578e-16 1.718297e-16
#> [13,] 7.937923e-19 6.642628e-18 -1.432033e-18 -4.806067e-17 2.298509e-17
#> [14,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [15,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [16,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [17,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [18,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [19,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [20,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [21,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [22,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [23,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [,11] [,12] [,13] [,14] [,15]
#> [1,] 4.329480e-18 9.981672e-18 -1.629385e-19 0.000000e+00 0.000000e+00
#> [2,] -2.849605e-18 -3.958199e-18 8.843864e-20 0.000000e+00 0.000000e+00
#> [3,] -6.941719e-19 1.834303e-17 -5.010109e-19 0.000000e+00 0.000000e+00
#> [4,] -3.540586e-17 4.468800e-18 3.526881e-19 0.000000e+00 0.000000e+00
#> [5,] -2.260428e-17 6.018597e-18 -3.690355e-19 0.000000e+00 0.000000e+00
#> [6,] -2.718100e-16 5.664200e-17 7.937923e-19 0.000000e+00 0.000000e+00
#> [7,] 3.025570e-16 -1.267454e-16 6.642628e-18 0.000000e+00 0.000000e+00
#> [8,] -7.113632e-18 2.024615e-17 -1.432033e-18 0.000000e+00 0.000000e+00
#> [9,] 1.087077e-15 -5.402578e-16 -4.806067e-17 0.000000e+00 0.000000e+00
#> [10,] -1.400184e-15 1.718297e-16 2.298509e-17 0.000000e+00 0.000000e+00
#> [11,] 1.000000e+00 -2.437609e-15 -2.325477e-16 -6.938885e-18 -4.112178e-17
#> [12,] -2.437609e-15 1.000000e+00 2.939043e-15 -4.150024e-16 -1.222252e-15
#> [13,] -2.325477e-16 2.939043e-15 1.000000e+00 -8.767934e-16 6.588478e-16
#> [14,] -6.938885e-18 -4.150024e-16 -8.767934e-16 1.000000e+00 -2.688308e-16
#> [15,] -4.112178e-17 -1.222252e-15 6.588478e-16 -2.688308e-16 1.000000e+00
#> [16,] 2.656958e-18 1.808320e-16 -5.469462e-17 3.040555e-17 1.118171e-16
#> [17,] -8.969883e-18 -1.901868e-16 5.880429e-16 -2.095378e-16 5.041938e-16
#> [18,] 2.507992e-17 -3.058981e-17 -5.969468e-16 1.088786e-16 -1.193167e-15
#> [19,] -2.475485e-18 -3.164968e-17 3.786323e-17 5.088476e-18 -4.002665e-17
#> [20,] 1.467867e-18 1.413369e-17 -2.797133e-17 0.000000e+00 0.000000e+00
#> [21,] -1.771076e-18 -5.199643e-18 1.318362e-17 0.000000e+00 0.000000e+00
#> [22,] 4.003676e-20 -6.498330e-18 1.363294e-18 0.000000e+00 0.000000e+00
#> [23,] -1.340072e-18 -8.852469e-18 4.329480e-18 6.488259e-19 3.456399e-17
#> [,16] [,17] [,18] [,19] [,20]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] 2.656958e-18 -8.969883e-18 2.507992e-17 -2.475485e-18 1.467867e-18
#> [12,] 1.808320e-16 -1.901868e-16 -3.058981e-17 -3.164968e-17 1.413369e-17
#> [13,] -5.469462e-17 5.880429e-16 -5.969468e-16 3.786323e-17 -2.797133e-17
#> [14,] 3.040555e-17 -2.095378e-16 1.088786e-16 5.088476e-18 0.000000e+00
#> [15,] 1.118171e-16 5.041938e-16 -1.193167e-15 -4.002665e-17 0.000000e+00
#> [16,] 1.000000e+00 -1.400200e-16 4.499366e-16 -1.099991e-17 0.000000e+00
#> [17,] -1.400200e-16 1.000000e+00 -1.283190e-15 1.478028e-16 -6.848967e-18
#> [18,] 4.499366e-16 -1.283190e-15 1.000000e+00 -8.073802e-16 5.054478e-16
#> [19,] -1.099991e-17 1.478028e-16 -8.073802e-16 1.000000e+00 -7.665030e-16
#> [20,] 0.000000e+00 -6.848967e-18 5.054478e-16 -7.665030e-16 1.000000e+00
#> [21,] 0.000000e+00 -1.821870e-17 -1.161446e-15 5.200541e-16 -4.195039e-16
#> [22,] 0.000000e+00 -1.176312e-17 -1.191137e-16 1.611974e-16 -2.649931e-16
#> [23,] -2.823535e-17 5.178255e-17 -9.062980e-16 2.074371e-16 1.269364e-17
#> [,21] [,22] [,23]
#> [1,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [2,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [3,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [4,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [5,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [6,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [7,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [8,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [9,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [10,] 0.000000e+00 0.000000e+00 0.000000e+00
#> [11,] -1.771076e-18 4.003676e-20 -1.340072e-18
#> [12,] -5.199643e-18 -6.498330e-18 -8.852469e-18
#> [13,] 1.318362e-17 1.363294e-18 4.329480e-18
#> [14,] 0.000000e+00 0.000000e+00 6.488259e-19
#> [15,] 0.000000e+00 0.000000e+00 3.456399e-17
#> [16,] 0.000000e+00 0.000000e+00 -2.823535e-17
#> [17,] -1.821870e-17 -1.176312e-17 5.178255e-17
#> [18,] -1.161446e-15 -1.191137e-16 -9.062980e-16
#> [19,] 5.200541e-16 1.611974e-16 2.074371e-16
#> [20,] -4.195039e-16 -2.649931e-16 1.269364e-17
#> [21,] 1.000000e+00 1.118171e-16 8.650947e-16
#> [22,] 1.118171e-16 1.000000e+00 -2.661877e-16
#> [23,] 8.650947e-16 -2.661877e-16 1.000000e+00
A=gramian(Sp=Sp$bs,Sp2=Sp$os) #cross-Gramian matrix, the coefficients of
#the decomposition of the B-splines
plot(Sp$bs)
 plot(lincomb(Sp$os,A))
plot(lincomb(Sp$os,A))