Any spline of a given order remains a spline of the same order if one considers it on a bigger set of knots than the original one.
However, this embedding changes the Splinets representation of the so-refined spline.
The function evaluates the corresponding Splinets-object.
Arguments
- object
Splinets-object, the object to be represented as aSplinets-object over a refined set of knots;- mult
positive integer, refining rate; The number of the knots to be put equally spaced between the existing knots.
- newknots
mvector, new knots; The knots do not need to be ordered and knots from the inputSplinets-object knots are allowed since any ties are resolved.
Value
A Splinet object with the new refined knots and the new matrix of derivatives is evaluated at the new knots combined with the original ones.
Details
The function merges new knots with the ones from the input object. It utilizes deriva()-function to evaluate the derivative at the refined knots.
It removes duplications of the refined knots, and account also for the not-fully supported case.
In the case when the range of the additional knots extends beyond the knots of the input Splinets-object,
the support sets of the output Splinets-object account for the smaller than the full support.
References
Liu, X., Nassar, H., Podg\(\mbox{\'o}\)rski, K. "Dyadic diagonalization of positive definite band matrices and efficient B-spline orthogonalization." Journal of Computational and Applied Mathematics (2022) <https://doi.org/10.1016/j.cam.2022.114444>.
Podg\(\mbox{\'o}\)rski, K. (2021)
"Splinets – splines through the Taylor expansion, their support sets and orthogonal bases." <arXiv:2102.00733>.
Nassar, H., Podg\(\mbox{\'o}\)rski, K. (2023) "Splinets 1.5.0 – Periodic Splinets." <arXiv:2302.07552>
Examples
#-------------------------------------------------#
#----Refining splines - the full support case-----#
#-------------------------------------------------#
k=3 # order
n = 16 # number of the internal knots (excluding the endpoints)
xi = seq(0, 1, length.out = n+2)
set.seed(5)
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1))
spl=construct(xi,k,S)
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> Spline 1 's highest derivative is not symmetrically defined at the center (the values at the two central knots should be equal).
#> Spline 1 's highest derivative values at the two central knots have been made equal by averaging the two central values in SLOT 'der'.
#>
#> The matrix of derivatives at the knots for spline 1 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 1.29923 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> The matrix derivative is now corrected by method RRM .
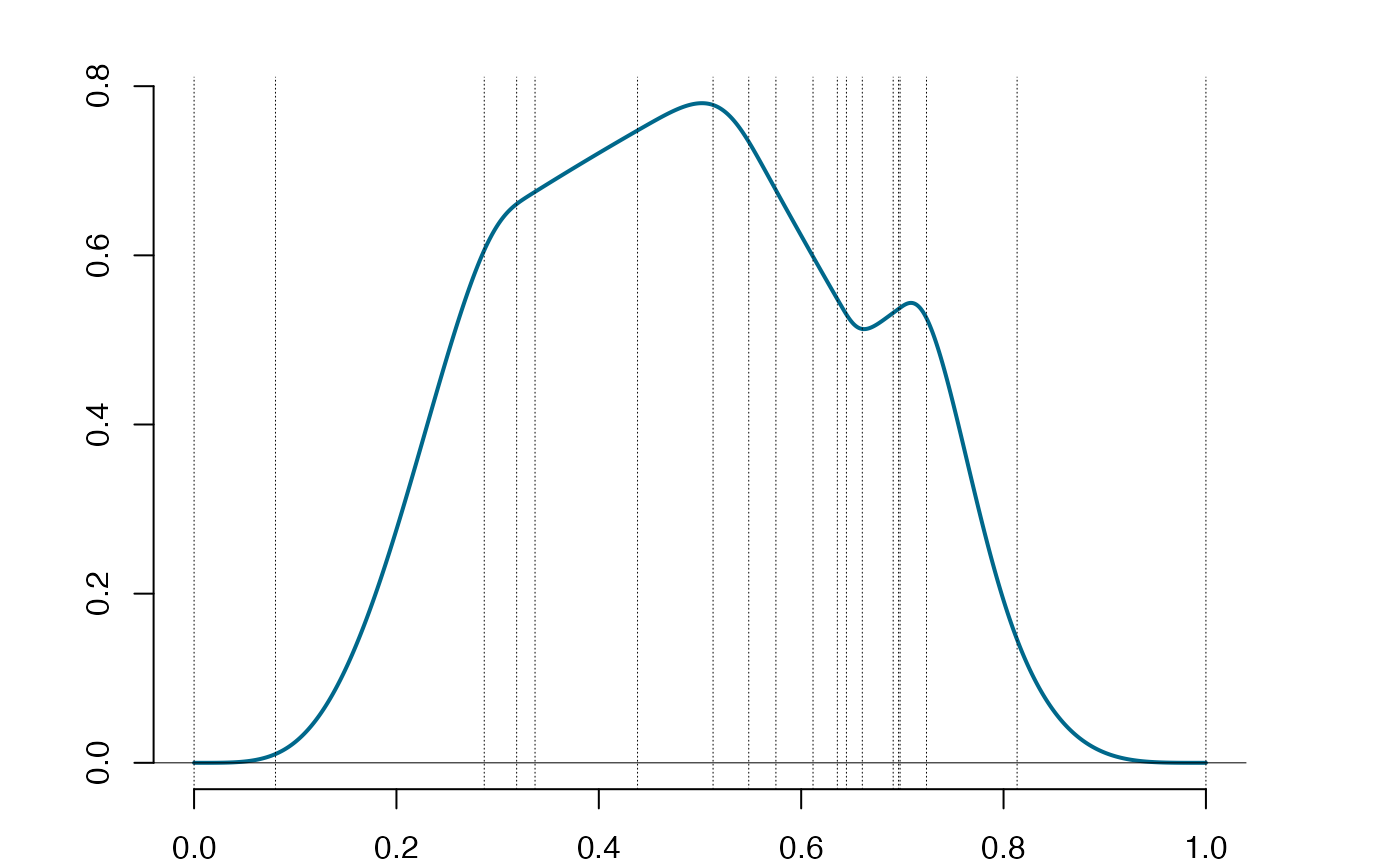
plot(spl) # plotting a spline
 rspl=refine(spl) # refining the equidistant by doubling its knots
plot(rspl)
rspl=refine(spl) # refining the equidistant by doubling its knots
plot(rspl)
 rspl@equid # the outcome is equidistant
#> [1] TRUE
#a non-equidistant case
n=17; k=4
xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1))
spl=construct(xi,k,S)
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The spline 1 'ths highest derivative at the central knot is zero.
#> Now it is set to zero.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.639126 .
#>
#>
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The matrix derivative is now corrected by method RRM .
plot(spl)
rspl@equid # the outcome is equidistant
#> [1] TRUE
#a non-equidistant case
n=17; k=4
xi=sort(runif(n+2)); xi[1]=0; xi[n+2]=1
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1))
spl=construct(xi,k,S)
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> The spline 1 'ths highest derivative at the central knot is zero.
#> Now it is set to zero.
#>
#> The derivative matrix for spline 1 does not satisfy the smoothness conditions (up to the accuracy SLOT 'epsilon').
#> The standard error per matrix entry is 1.639126 .
#>
#>
#> Correction of the LHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the RHS part of the matrix
#> There are less than 6 knots, the first 1 entries of the 6 nd row counting from the end in the input will be changed in the output.
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object has the derivative matrix corrected by the RRM method.
#>
#> The matrix derivative is now corrected by method RRM .
plot(spl)
 mult=3 #adding two knots between each subsequent pair of the original knots
rspl=refine(spl,mult)
is.splinets(rspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 55 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 8.399186e-19
#>
plot(rspl)
mult=3 #adding two knots between each subsequent pair of the original knots
rspl=refine(spl,mult)
is.splinets(rspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 55 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 8.399186e-19
#>
plot(rspl)
 #adding specific knots
rspl=refine(spl,newknots=c(0.5,0.75))
rspl@knots
#> [1] 0.00000000 0.08046064 0.28675657 0.31881230 0.33696592 0.43827330
#> [7] 0.50000000 0.51291065 0.54819018 0.57502166 0.61170086 0.63571503
#> [13] 0.64470537 0.66039129 0.69090463 0.69626323 0.69773493 0.72383933
#> [19] 0.75000000 0.81337853 1.00000000
is.splinets(rspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 21 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 8.399072e-19
#>
plot(rspl)
#adding specific knots
rspl=refine(spl,newknots=c(0.5,0.75))
rspl@knots
#> [1] 0.00000000 0.08046064 0.28675657 0.31881230 0.33696592 0.43827330
#> [7] 0.50000000 0.51291065 0.54819018 0.57502166 0.61170086 0.63571503
#> [13] 0.64470537 0.66039129 0.69090463 0.69626323 0.69773493 0.72383933
#> [19] 0.75000000 0.81337853 1.00000000
is.splinets(rspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 21 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: The full support range for each spline.
#> $Er
#> [1] 8.399072e-19
#>
plot(rspl)
 #----------------------------------------------------#
#----Refining splines - the partial support case-----#
#----------------------------------------------------#
Bases=splinet(xi,k)
plot(Bases$bs)
#----------------------------------------------------#
#----Refining splines - the partial support case-----#
#----------------------------------------------------#
Bases=splinet(xi,k)
plot(Bases$bs)
 Base=Bases$bs
BS_Two=subsample(Bases$bs,c(1,length(Base@der)))
plot(BS_Two)
Base=Bases$bs
BS_Two=subsample(Bases$bs,c(1,length(Base@der)))
plot(BS_Two)
 A=matrix(c(1,-1),ncol=2)
spl=lincomb(BS_Two,A)
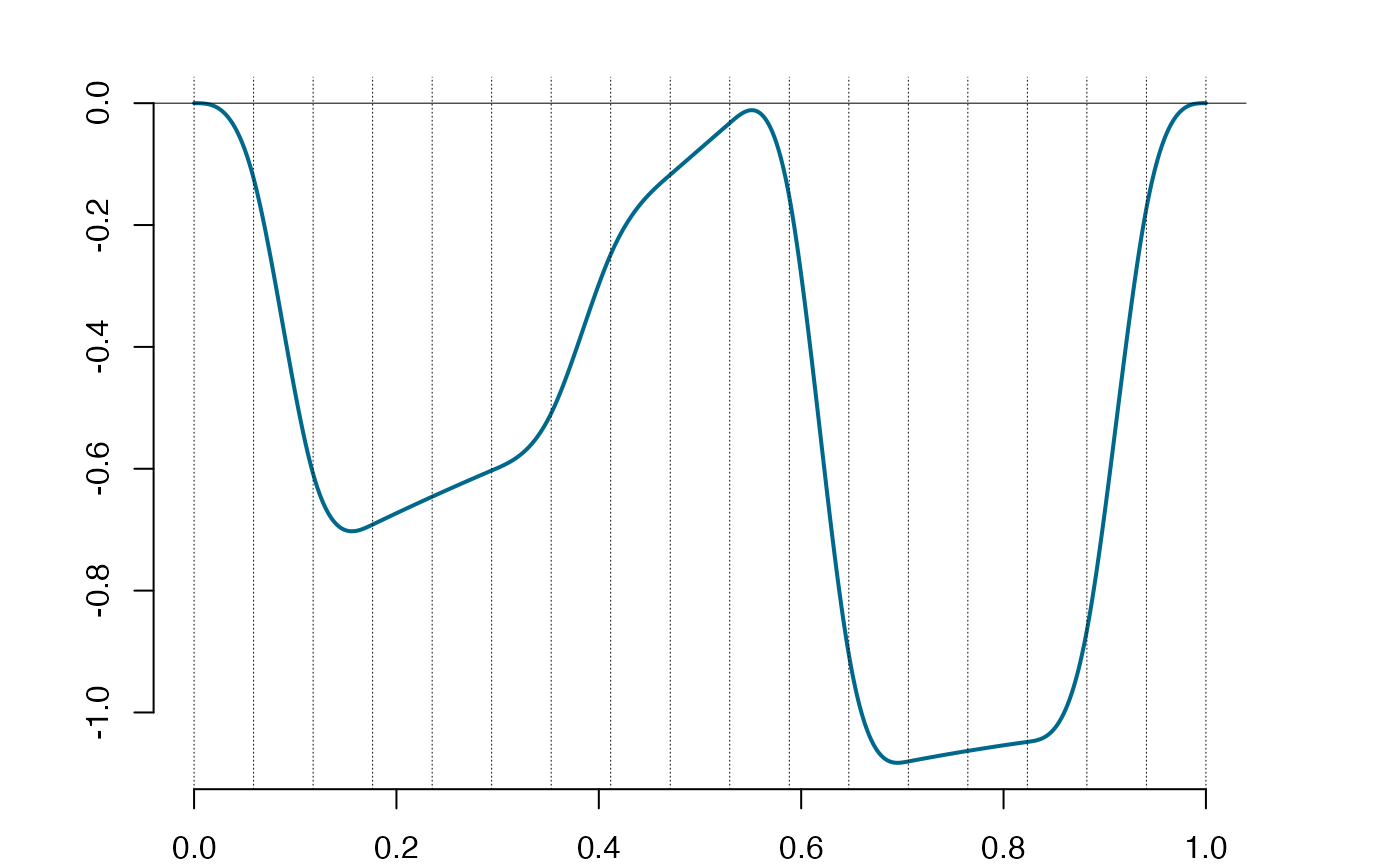
rspl=refine(spl) #doubling the number of knots
plot(rspl)
A=matrix(c(1,-1),ncol=2)
spl=lincomb(BS_Two,A)
rspl=refine(spl) #doubling the number of knots
plot(rspl)
 is.splinets(rspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 37 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: Not the full range support, the number of support intervals varies from 2 to 2
#> $Er
#> [1] 1.50215e-19
#>
rspl@supp #the support is evaluated
#> [[1]]
#> [,1] [,2]
#> [1,] 1 11
#> [2,] 27 37
#>
spl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 1 6
#> [2,] 14 19
#>
#The case of adding knots explicitely
BS_Middle=subsample(Bases$bs,c(floor(length(Base@der)/2)))
spls=gather(spl,BS_Middle)
plot(spls)
is.splinets(rspl)
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> $is
#> [1] TRUE
#>
#> $robject
#> splines
#> Knots: 37 non-equaly distributed knots between 0 and 1
#> Size: 1 spline functions
#> Order: 4
#> Support: Not the full range support, the number of support intervals varies from 2 to 2
#> $Er
#> [1] 1.50215e-19
#>
rspl@supp #the support is evaluated
#> [[1]]
#> [,1] [,2]
#> [1,] 1 11
#> [2,] 27 37
#>
spl@supp
#> [[1]]
#> [,1] [,2]
#> [1,] 1 6
#> [2,] 14 19
#>
#The case of adding knots explicitely
BS_Middle=subsample(Bases$bs,c(floor(length(Base@der)/2)))
spls=gather(spl,BS_Middle)
plot(spls)
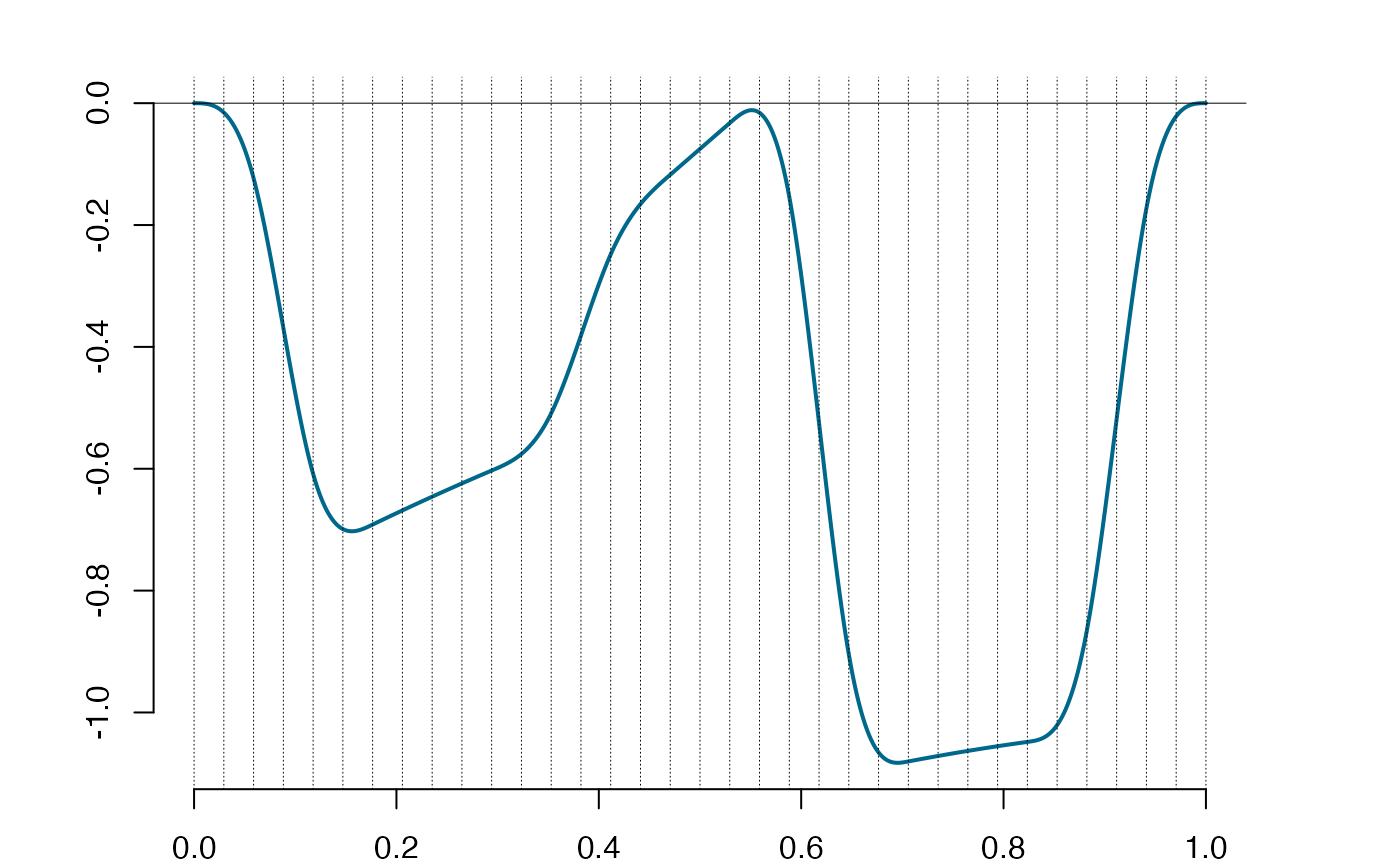
 rspls=refine(spls, newknots=c(0.2,0.5,0.85)) #two splines with partial support sets
#by adding three knots to B-splines
plot(rspls)
rspls=refine(spls, newknots=c(0.2,0.5,0.85)) #two splines with partial support sets
#by adding three knots to B-splines
plot(rspls)
 #----------------------------------------------------#
#------Refining splines over the larger range--------#
#----------------------------------------------------#
k=4 # order
n = 25 # number of the internal knots (excluding the endpoints)
xi = seq(0, 1, length.out = n+2)
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1))
spl=construct(xi,k,S)
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> Spline 1 's highest derivative at the central knot is not equal to zero.
#> Spline 1 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 1.366301 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> The matrix derivative is now corrected by method RRM .
plot(spl) # plotting a spline
#----------------------------------------------------#
#------Refining splines over the larger range--------#
#----------------------------------------------------#
k=4 # order
n = 25 # number of the internal knots (excluding the endpoints)
xi = seq(0, 1, length.out = n+2)
S=matrix(rnorm((n+2)*(k+1)),ncol=(k+1))
spl=construct(xi,k,S)
#>
#> Using method RRM to correct the derivative matrix entries.
#>
#>
#> DIAGNOSTIC CHECK of a SPLINETS object
#>
#> THE KNOTS:
#>
#>
#> THE SUPPORT SETS:
#>
#> The support sets for the splines are equal to the entire range of knots.
#>
#>
#> THE DERIVATIVES AT THE KNOTS:
#>
#> The boundary zero conditions are not satisfied for spline 1 in the input 'Splinets' object.
#> Correction of the first and last rows of the derivative matrices are made in the output 'Splinets' object.
#>
#> Spline 1 's highest derivative at the central knot is not equal to zero.
#> Spline 1 's highest derivative value at the central knot has been made equal to zero.
#>
#> The matrix of derivatives at the knots for spline 1 does not satisfy the conditions
#>
#> required for a spline (up to the accuracy SLOT 'epsilon').
#>
#> One of the reasons can be that SLOT 'taylor' is not correctly given.
#> The computed standard error per matrix entry is 1.366301 .
#>
#>
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> Correction of the LHS part of the matrix
#> Correction of the RHS part of the matrix
#> The output object Spline 1 has the derivative matrix corrected by the RRM method
#> given that SLOT 'taylor' is properly given.
#> The matrix derivative is now corrected by method RRM .
plot(spl) # plotting a spline
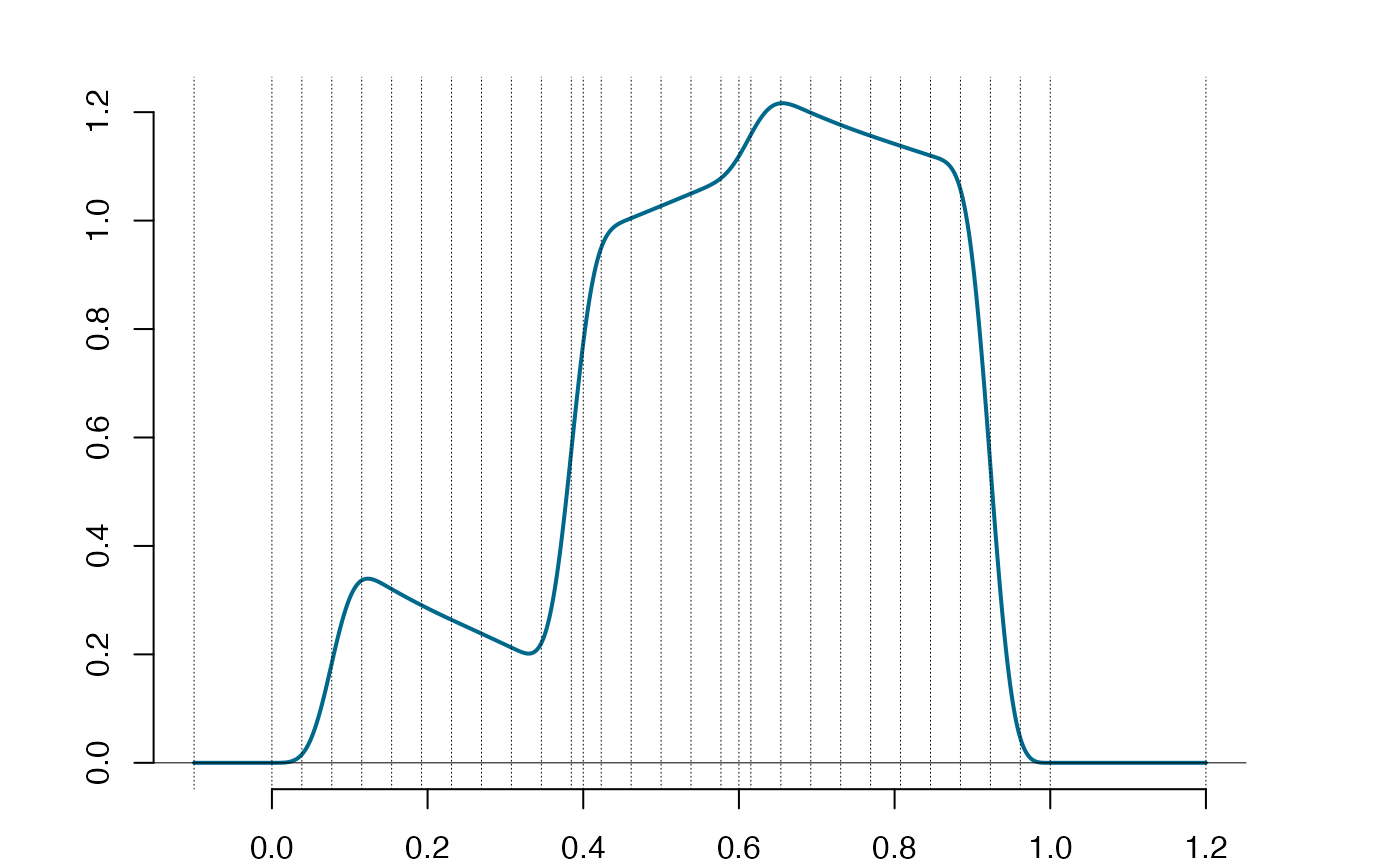
 newknots=c(-0.1,0.4,0.6,1.2) #the added knots create larger range
rspl=refine(spl,newknots=newknots)
spl@supp #the original spline has the full support
#> list()
rspl@supp #the embedded spline has partial support
#> [[1]]
#> [,1] [,2]
#> [1,] 2 30
#>
spl@equid
#> [1] TRUE
rspl@equid
#> [1] FALSE
plot(rspl)
newknots=c(-0.1,0.4,0.6,1.2) #the added knots create larger range
rspl=refine(spl,newknots=newknots)
spl@supp #the original spline has the full support
#> list()
rspl@supp #the embedded spline has partial support
#> [[1]]
#> [,1] [,2]
#> [1,] 2 30
#>
spl@equid
#> [1] TRUE
rspl@equid
#> [1] FALSE
plot(rspl)